图论
基础:DFS,BFS
简单:拓扑排序,有向无环图,最短路,并查集,最小生成树
中等:网络流,tarjan 算法,树上技术
苦难:仙人掌问题,建图
图的定义和概念🧐
图可以表示为一个二元组G = <V, E>,其中
V 表示非空顶点集,其元素称为顶点(Vertex)
E 表示边集,其元素称为边(Edge)
e = (u, v) 表示一条边,其中 u∈V, v∈V, e∈E
分类
相邻(Adjacent):边(u, v) 连接的顶点u和v相邻
关联(Incident):边(u, v) 和其连接的顶点u(或v)相互关联
度
顶点的度(Degree of a Vertex)
顶点v 的度 deg(v) 是 v 关联的边数
图的度(Degree of a Graph)
图 G = <V, E> 的度,是图各顶点的度之和,
握手定理
无向图的度是边数的两倍,deg(E) = 2|E|
在无向图中,「度」就是每个节点相连的边的条数。由于有向图的边有方向,所以有向图中每个节点「度」被细分为入度 (indegree)和出度 (outdegree)
路径(Path)
图中一个顶点序列
路劲包含顶点
存在路径
如果
环路(Cycle)
如果路径
如果
连通(Connectivity)
如果图的任意对顶点相互可达,则称该图是连通的,反之称为非联通
连通分量(Connected
Components)根据是否连通将顶点进行分组,相互可达的顶点集称为连通分量
子图(Subgraph)
如果𝑽′ ⊆ 𝑽, 𝑬′ ⊆ 𝐄,则称图𝑮’ =< 𝑽’, 𝑬’ >是图𝑮的一个子图
树(Tree) :连通、无环图𝑻 =< 𝑽𝑻, 𝑬𝑻
>,树有|𝑽𝑻| − 𝟏条边
森林(Forest) :一至多棵树组成的无环图
图的表示
邻接链表
图𝑮 =< 𝑽, 𝑬 > ,其邻接链表由|𝑽|条链表的数组构成
每个顶点有一条链表,包含所有与其相邻的顶点
𝑨𝒅𝒋[𝒂] = {𝒃, 𝒅} ; 𝑨𝒅𝒋[𝒃] = {𝒂, 𝒄, 𝒅, 𝒇} ; 𝑨𝒅𝒋[𝒄] = {𝒃, 𝒇};
...
空间大小 𝑶(|𝑽| + |𝑬|)
邻接矩阵
图的算法题 🤔
图算法经典问题📓
dfs深度优先搜索
具体算法描述:
选择一个起始点 u 作为 当前节点,执行如下操作:
访问 当前节点,并且标记当前节点已被访问,然后跳转到 b
如果存在一个和 当前节点 相邻且尚未被访问的节点 v,则将 v
设为当前节点,继续执行a
如果不存在这样的 v,则进行回溯,回溯的过程就是回退 当前节点
上述所说的 当前节点
需要用一个栈来维护,每次访问到的节点入栈,回溯的时候出栈。除了栈,另一种实现深度优先搜索的方式是
递归 ,代码更加简单,相对好理解。
拓扑排序
定义:给定一个包含 n 个节点的有向图
G,我们给出它的节点编号的一种排序,如果满足:对于图G中的任意一条有向边(u, v),u在排列中都出现在 v 的前面。那么称该排列是图
G 的拓扑排序 。
结论:
如果图G中存在环 (即图G不是有向无环图) ,那么图G
不存在拓扑排序。这是因为假设图中存在环
如果图G是有向无环图,那么它的拓扑排序可能不止一种。举一个最极端的例子,如果图G只包含n个节点却没有任何边,那么任意一种编号的排列都可以作为拓扑排序。
🤖拓扑排序的框架:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 #include <iostream> #include <vector> #include <queue> using namespace std;vector<int > adj[100001 ]; int inDegree[100001 ];void topologicalSort (int n) queue<int > q; for (int i = 1 ; i <= n; i++) { if (inDegree[i] == 0 ) { q.push (i); } } while (!q.empty ()) { int u = q.front (); q.pop (); cout << u << " " ; for (int v : adj[u]) { inDegree[v]--; if (inDegree[v] == 0 ){ q.push (v); } } } } int main () int n, m; cin >> n >> m; for (int i = 0 ; i < m; i++) { int u, v; cin >> u >> v; adj[u].push_back (v); inDegree[v]++; } topologicalSort (n); return 0 ; }
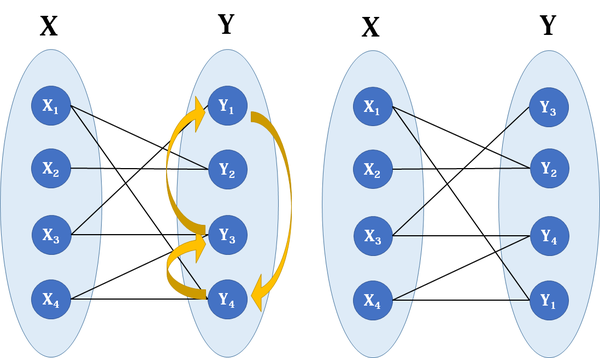
二分图
二分图:二分图的顶点集可分割为
两个互不相交的子集 ,图中 每条边 依附的两个顶点
都分属于这两个子集,且两个子集内的顶点不相邻。
问题转换:图的 [双色问题]
匈牙利算法
匈牙利算法,即图论中寻找最大匹配的算法,主要用于解决一些二分图匹配有关的问题。
基本概念
匹配 :匹配是边的集合,在集合中,任意两条边不能有共同的顶点。
最大匹配 :最大匹配的边数称为最大匹配。
完美匹配 :如果一个匹配中,每个顶点都和图中某条边关联,则称此为完美匹配。两个集合能
一 一 映射。
最优匹配 (带权最大匹配):在带有权值边的二分图中,求一个匹配使得匹配边上的权值和最大。KM算法是一种解决二分图最大权匹配问题的算法,也称为匈牙利算法的优化版。
最小覆盖 :最小覆盖分为 最小顶点覆盖
和 最小路径覆盖 :
最小顶点覆盖是指 最少的顶点数 使得
二分图G的每条边都至少与其中的一个点关联,二分图的最小顶点覆盖数
等于 二分图的最大匹配数 。
最小路径覆盖 也成为
最小边覆盖,是指用尽量少的不相交的简单路径覆盖二分图中所有的顶点。二分图的最小路径覆盖数
= 顶点数 - 二分图的最大匹配数 。
最大独立集 :寻找一个点集,使得其中任意两点在图中无对应边。对于一般图来说,最大独立集是一个
NP完全问题,对于二分图来说:最大独立集 = 定点数 -
二分图的最大匹配数 。
交替路 :如果一条路径的第一条边是匹配边,那么第二条边就必须是非匹配边,第三条边又必须是匹配边,以此类推。这样的路径被称为交替路。
增广路 (增广轨 或
交错轨):指一条从未匹配的左侧顶点出发,经过一系列交替的匹配边和非匹配边,最终到达未匹配的右侧顶点的路径。具体来说,增广路的第一条边必须是非匹配边,接下来的每一条边都必须交替地是匹配边和非匹配边,最后一条边必须是非匹配边。
匈牙利算法的思路就是:通过不断寻找增广路,可以不断增加匹配的大小,从而找到最大匹配。
算法概述
匈牙利算法主要用于解决 二分图的最大匹配数 和
最小点覆盖数 。
二分图的最大匹配数问题 :在二分图中
最多 能找到多少条
没有公共端点的边 。
具体实现过程:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 int M, N; int Map[MAXN][MAXN]; int p[MAXN]; bool vis[MAXN]; bool match (int i) for (int j = 1 ; j<=N; j++) { if (Map[i][j] && !vis[j]) { vis[j] = true ; if (p[j] == 0 || mathch (p[j])) { p[j] = i; return true ; } } } return false ; } int Hungarian () int cnt = 0 ; for (int i = 1 ; i<=M; i++) { memset (vis, 0 , sizeof (vis)); if (mathch (i)) cnt++; } return cnt; }
最小点覆盖问题 :找到最少数量的点,使得二分图所有的边都至少有一个端点在这些点之中。
我们只需要一个结论:一个二分图的最大匹配数 =
这个图中的最小覆盖数 (König定理)。
并查集
主要用于解决一些 元素分组 的问题,它管理一系列
不相交的集合,并支持两种操作:
合并(Union):把两个不相交的集合 合并 为一个集合
查询(Find):查询两个元素是否在同一个集合中
并查集的重要思想在于:用集合中的一个元素代表集合。
初始化
1 2 3 4 5 6 int fa[MAXN];inline void init (int n) for (int i = 1 ; i<=n; i++){ fa[i] = i; } }
假设有 编号为1,2,...,n 的 n个元素,我们用一个数组 fa[]
来存储每个元素的父节点(因为每个元素有且只有一个父节点,所以这是可行的)。一开始,我们将它们的父节点设为自己。
查询
1 2 3 4 int find (int x) if (fa[x] == x) return x; else return find (fa[x]); }
一层一层访问父节点,直至根节点(根节点的标志就是父节点本身)。要判断两个元素是否属于同一个集合,只要看它们的根节点是否相同即可。
合并
1 2 3 inline void merge (int i, int j) fa[find (i)] = find (j); }
合并操作:先找到两个集合的代表元素,然后将前者的父节点设置为后者即可。当然也可以将后者的父节点设为前者。
合并·路径压缩
路径压缩:把沿途每个节点的父节点都设为根节点,提高并查集查找效率
1 2 3 int find (int x) return x == fa[x]?x:(fa[x] = find (fa[x])); }
按秩合并
由于路径压缩只在查询时进行,也只压缩一条路径,所以并查集最终的结构仍然可能是比较复杂的。
当复杂的树与简单的树合并时,应该将简单的树往复杂的树上合并。
用一个数组 rand[]
记录每个根节点对应树的深度(如果不是根节点,其rank相当于以它作为根节点的子树的深度)。一开始把所有元素的rank(秩)设为1。合并时比较两个根节点,把
rank较小者往较大者上合并。
路径压缩和按秩合并一起使用,时间复杂度为O(n),但很可能破坏 rank
的准确性
初始化(按秩合并)
1 2 3 4 5 6 inline void init (int n) for (int i = 1 ; i<=n; i++){ fa[i] = i; rank[i] = 1 ; } }
合并(按秩合并)
1 2 3 4 5 6 7 8 9 inline void merge (int i, int j) int x = find (i), y = find (j); if (rank[x] <= rank[y]) fa[x] = y; else fa[y] = x; if (rank[x] == rank[y] && x!=y) rank[y]++; }
最小生成树
给定一张边带权的无向图 G = (V, E), n = |V|, m = |E|。由 V 中全部 n
个顶点和 E 中 n-1条边构成的无向连通子图称为 G
的一棵生成树。边的权值之和最小的生成树被称为无向图 G 的最小生成树。
定理:任意一棵最小生成树一定包含无向图中权值最小的边
树:无环连通图
img
两种算法(思路)
Kruskal 算法
将所有路径排序,然后选取 n-1 条路径,具体选法
先选择最小边,此时集合中有两个节点
选取下一条的原则:FIRST 最小 SECOND
是在集合中的节点与剩余节点之间,不能形成回路
重复 n-1 次
算法流程:
建立并查集,每个点各自构成一个集合
把所有边按照权值从小到达排序,依次扫描每条边(x,y,z)
若 x, y 属于同一集合(连通),则忽略这条边,继续扫描下一条
否则,合并 x, y所在的集合,并把 z 累加到答案中
所有边扫描完成后,第4步中处理过的边就构成最小生成树
时间复杂度
算法模板:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 struct Edge { int x, y, len; bool operator < (Edge& other) { return len < other.len; } }edge[10000 ]; int fa[10000 ], n, m, ans;int find (int x) if (fa[x] == x) return x; return find (fa[x]); } int main () cin >> n >> m; for (int i = 1 ; i<=m; i++) { cin >> edge[i].x >> edge[i].y >> edge[i].len; } sort (edge+1 , edge+m+1 ); for (int i = 1 ; i<=n; i++) fa[i] = i; for (int i = 1 ; i<=m; i++) { int x = find (edge[i].x); int y = find (edge[i].y); if (x == y) continue ; fa[x] = y; ans += edge[i].z; } cout << ans << endl; }
Prim 算法
随机选择一个点P
遍历与P连通的点,找到最小路径连接的另一个点,这个点必须是还没有访问过,将该点加入集合,记录添加的边。
把与当前集合可以访问的所有边和点,选一个最短路径连接的点在纳入集合,如此重复,直到没有新的点可以加入
此时所有边构成的树为最小生成树
算法示例:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 int a[1000 ][1000 ], dist[1000 ], n, m, ans;bool in[1000 ];void prim () memset (dist, 0x3f , sizeof (dist)); memset (in, 0 , sizeof (in)); dist[1 ] = 0 ; for (int i = 1 ; i<n; i++) { int x = 0 ; for (int j = 1 ; j<=n; j++) if (!in[j] && (x == 0 || dist[j]<dist[x])) x = j; in[x] = true ; for (int y = 1 ; y<=n; y++) { if (!in[y]) dist[y] = min (dist[y], a[x][y]); } } } int main () cin >> n >> m; memset (a, 0x3f , sizeof (a)); for (int i = 1 ; i<=n; i++) a[i][i] = 0 ; for (int i = 1 ; i<=m; i++) { int x, y, len; cin >> x >> y >> len; a[x][y] = a[y][x] = min (a[x][y], z); } prim (); for (int i = 2 ; i<=n; i++) ans+=dist[i]; cout << ans << endl; }
Dijkstra 算法
其主要思想是贪心,具体地说:
将所有节点分成两类:已确定从起点到当前点的最短路长度的节点,以及未确定从起点到当前点的最短路长度的节点(下面简称「未确定节点」和「已确定节点」)。
每次从「未确定节点」中取一个与起点距离最短的点 ,将它归类为「已确定节点」,并用它「更新 」从起点到其他所有「未确定节点」的距离。直到所有点都被归类为「已确定节点」 。
用节点 A「更新」节点 B 的意思是,用 起点到节点 A 的最短路长度
加上 从节点 A 到节点 B 的边的长度,去比较 起点到节点 B
的最短路长度,如果前者小于后者,就用前者更新后者。这种操作也被叫做「松弛」。
Dijkstra
算法基本策略:使用邻接列表来表示图,查找从起始顶点到所有其他顶点的最短路径,优先级队列用于在每次迭代中有效地选择距离最小的顶点。
🤖代码框架:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 vector<int > dijkstra (vector<vector<pair<int , int >>>& graph, int start) { int n = graph.size (); vector<int > dist (n, INT_MAX) ; priority_queue<pair<int , int >,vector<pair<int , int >> ,greater<pair<int , int >>> pq; dist[start] = 0 ; pq.push ({0. start}); while (!pq.empty ()){ int u = pq.top ().second; int d = pq.top ().first; pq.pop (); if (d > dist[u]) continue ; for (auto & edge: graph[u]){ int v = edge.first; int w = edge.second; if (dist[u]+w < dist[v]){ dist[v] = dist[u]+w; pq.push ({dist[v], v}); } } } return dist; }
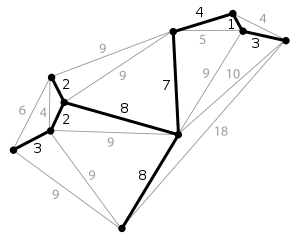
例图:
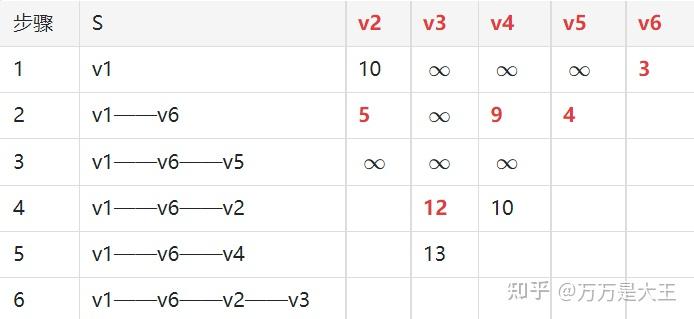
SPFA 算法
SUMMARY
初始化除源顶点为0之外的所有顶点的无限距离数组。
创建一个空队列,并将源顶点加入其中。
如果队列不为空,执行如下操作:
删除队列最前面的顶点。
对于该顶点的每个邻居,计算到它的距离(即到当前顶点的距离+它们之间边的权重)。c.
如果该距离小于邻居的当前距离,则更新距离数组,并将该邻居加入队列(如果它尚未在队列中)。
重复第3步,直到队列为空或所有顶点都被访问过。
distance数组现在包含了从源顶点到图中所有其他顶点的最短距离。
🤖以下是SPFA算法的框架,使用C++编写:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 const int INF = 1e9 ;const int MAXN = 100005 ;vector<pair<int , int >> adj[MAXN]; int dist[MAXN];bool inQueue[MAXN];void SPFA (int start) queue<int > q; memset (dist, INF, sizeof (dist)); memset (inQueue, false , sizeof (inQueue)); dist[start] = 0 ; q.push (start); inQueue[start] = true ; while (!q.empty ()) { int u = q.front (); q.pop (); inQueue[u] = false ; for (auto v : adj[u]) { if (dist[v.first] > dist[u] + v.second) { dist[v.first] = dist[u] + v.second; if (!inQueue[v.first]) { q.push (v.first); inQueue[v.first] = true ; } } } } }
在这个实现中,adj是一个邻接表,表示图中的边,其中每个元素是一个形如(v, w)的对,表示从当前节点到节点v有一条权重为w的边。dist是一个数组,存储从起点到图中每个节点的最短距离。inQueue是一个布尔数组,用于记录一个节点当前是否在队列中。
SPFA函数以起点作为输入,使用队列进行最短路径搜索。它将所有节点的距离初始化为无穷大,除了起点,起点的距离为0。然后将起点加入队列,并将其inQueue标志设置为true。
然后,函数进入一个循环,直到队列为空为止。在每次迭代中,它从队列中取出一个节点u,将其inQueue标志设置为false。然后检查u的所有邻居,并在找到更短的路径时更新它们的距离。如果邻居的距离被更新,则函数检查它是否已经在队列中。如果不在,则将其加入队列,并将其inQueue标志设置为true。
最后,main函数读取输入,调用SPFA函数,并输出图中所有节点的最短距离。如果一个节点从起点不可达,则输出其距离为“INF”。
SPFA算法和Dijkstra算法的差别
SPFA算法和Dijkstra算法都是用于在加权图中寻找最短路径的算法。但是,它们之间有一些不同之处:
时间复杂度:Dijkstra算法使用优先队列,其时间复杂度为O(ElogV),其中E是边数,V是顶点数。另一方面,SPFA算法的最坏时间复杂度为O(VE),比Dijkstra算法慢。但是,在实践中,SPFA算法在
稀疏图 上的表现通常比Dijkstra算法好。
负权重:Dijkstra算法不能处理图中的负权重,因为它假设所有边的权重都是非负的。另一方面,SPFA算法可以处理负权重,但如果图中包含负环,则可能无法终止。
内存使用:Dijkstra算法需要使用优先队列来存储顶点,这可能会对大型图形成内存压力。SPFA算法使用简单的队列,需要更少的内存。
优化:Dijkstra算法可以使用斐波那契堆或桶队列等技术进行优化,以提高其性能。SPFA算法没有太多可用的优化技术,因为它已经是一个简单的算法。
总之,Dijkstra算法在大多数图形上比SPFA算法更快,更节省内存,但不能处理负权重。SPFA算法可以处理负权重,但在某些图形上可能比Dijkstra算法慢,内存效率低。
A* 算法
A*算法的主要框架如下:
初始化起始节点,其代价为0。
创建一个开放列表,并将起始节点添加到其中。
创建一个关闭列表。
当开放列表不为空时: a. 从开放列表中选择具有最低f值(f = g +
h,其中g是从起始节点到当前节点的代价,h是当前节点到目标节点的估算代价)的节点。
b. 如果选择的节点是目标节点,则已找到最短路径。返回路径。 c.
否则,将所选节点从开放列表中删除并将其添加到关闭列表中。 d.
对于所选节点的每个邻居: i. 如果邻居已经在关闭列表中,则跳过。 ii.
计算邻居的g值,作为从起始节点到邻居节点经过所选节点的代价。 iii.
如果邻居不在开放列表中,则将其添加到开放列表中,并将其h值计算为从邻居到目标节点的估算代价。
iv.
如果邻居已经在开放列表中,并且它的新g值低于旧的g值,则更新其g值,并更新其父节点为所选节点。
如果开放列表为空且未找到目标节点,则从起始节点到目标节点没有路径。返回失败。
floyd算法
Floyd算法 是解决任意两点间的最短路径的一种算法 是一种插点算法
可以正确处理有向图或带负权非回路的最短路径算法
同时也被用于计算有向图的传递闭包 Floyd时间复杂度为动态规划 的多源最短路算法。
最优子结构:图结构中一个显而易见的定理:最短路径的子路径仍然是最短路径 。
一般的动态规划,设定 dist[k][i][j] 为经过前 k
的节点,从i 到 j 所得到的最短路径,dist[k][i][j] 可以从
dist[k-1][i][k]+dist[k-1][k][j]
转移过来,可以看出,k的状态完全由 k-1 转移过来,只要 将 k
的循环放在最外层就能保证无后效行。最后得到
dist[k][j][i] = min(dist[k-1][i][k]+dist[k-1][k][j], dist[k][j][i])
。
观察可知,可以用 滚动数组
进行优化,降低空间复杂度。分析可知 dist[i][j] 依赖于
f[i][k]+dist[k][j],在更新dist[m][n]时,用到dist[m][k]+dist[k][n]。
最终的方程:dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])
🤖算法框架:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 void floyd (vector<vector<int >>& graph) int n = graph.size (); vector<vector<int >> dist (n, vector <int >(n, 0 )); for (int i = 0 ; i < n; i++) { for (int j = 0 ; j < n; j++) { dist[i][j] = graph[i][j]; } } for (int k = 0 ; k < n; k++) { for (int i = 0 ; i < n; i++) { for (int j = 0 ; j < n; j++) { if (dist[i][k] != INT_MAX && dist[k][j] != INT_MAX && dist[i][k] + dist[k][j] < dist[i][j]) { dist[i][j] = dist[i][k] + dist[k][j]; } } } } }
如何找到具体的路径呢?在 Floyd 算法中,只需要在更新
dist[i][j]的时候,更新中间节点就可以了。
1 2 3 4 if (dist[i][k] != INT_MAX && dist[k][j] != INT_MAX && dist[i][k] + dist[k][j] < dist[i][j]) { dist[i][j] = dist[i][k] + dist[k][j]; path[i][j] = k; }
打印路径
1 2 3 4 5 6 7 8 string getPath (vector<vector<int >>& path, int i, int j) { if (path[i][j] == -1 ){ return " " +i+" " +j; }else { int k = path[i][j]; return getPath (path, i, k)+" " +getPath (path, k, j)+" " ; } }
注 :Floyd
算法只能在不存在负权环 的情况下(可以有负权值)使用,因为其并不能判断负权环,如果有负权环,最短路将无意义。
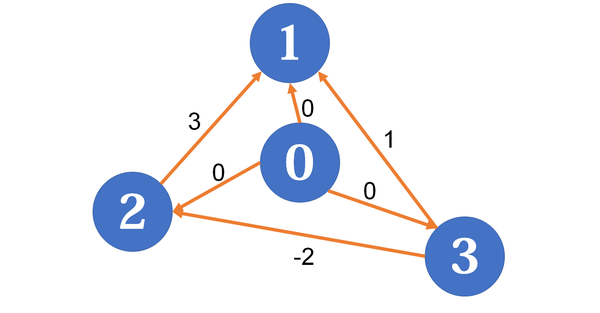
差分约束算法
差分约束系统是下面这种形式的多元一次不等式组(
(每个不等式称为一个约束条件,都是两个未知量之差小于或等于某个常数)很多题目都会给出一系列不等关系,我们都可以尝试把它们转化为差分约束系统来解决。
问题转化
我们设 最短路问题
中的 三角不等式
这样建出的
有向图 ,它的每个顶点都对应差分约束系统中的一个未知量,源点到每个顶点的最短路对应这些未知量的值 ,而每条
边 对应一个 约束条件。
那么既然是最短路,源点在哪?实际上取哪个点为源点无关紧要,但是有时候得到的图不连通,这样求出的结构很容易出现
INF。为了避免这种情况,我们人为增加一个 超级源点 。
例如在上面的图中人为增加一个 0 号点(或 n+1
号点),从它向所有顶点连一条边权为 0 的边:
现在我们以 0
号点为源点求各点的最短路即可。注意这相当于添加了以下约束条件:
由于
在有解的情况下,最短路的答案
连边方法
差分约束问题可以转化为 最短路 或
最长路问题,所以两种转化也就成了两种不同的连边方法。
如果图存在负环,如果一直沿着负环走,最短路径将会越来越小,最后到达
此时,可以使用 SPFA,只需要在使用 SPFA
的同时用一个数组来记录每个顶点入队次数,如果一个顶点入队次数大于
n,说明该图存在负环。
解决方案
一、SPFA
一开始将所有点放入队列 中而不是只放一个起点,这样每个点都被作为起点讨论过。建一个虚拟源点 0,从这个虚拟源点向其他所有点都连一条长度为 0
的边,以虚拟源点为起点放入队列 ,这样的效果与前一种完全相同。
二、Bellman-Ford
无需操作 ,算出来的答案本来就是正确的。
因为每次松弛是对所有边进行操作 ,不会出现只计算一个连通块的情况。
代码
最短路 + SPFA
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 #include <iostream> #include <vector> #include <queue> #include <climits> using namespace std;vector<vector<pair<int , int >>> graph; vector<int > dis; int n, m;bool spfa () vector<bool > inque (n+1 , false ) ; vector<int > vis (n+1 , 0 ) ; queue<int > q; q.push (0 ); dis[0 ] = 0 , vis[0 ] = 1 ; while (!q.empty ()) { int cur = q.front (); q.pop (); inque[cur] = false ; for (int i = 0 ; i<graph[cur].size (); i++) { int nx = graph[cur][i].first; int len = graph[cur][i].second; if (dis[nx] > dis[cur] + len) { dis[nx] = dis[cur]+len; if (!inque[nx]) { q.push (nx); inque[nx] = true ; vis[nx]++; if (vis[nx] > n+1 ) return false ; } } } } return true ; } int main () cin >> n >> m; graph.resize (n+1 ), dis.resize (n+1 ), dis.assign (n+1 , INT_MAX); while (m--) { int a, b, c; cin >> a >> b >> c; graph[b].emplace_back (a, c); } for (int i = 1 ; i<=n; i++) { graph[0 ].emplace_back (i, 0 ); } if (!spfa ()) cout << "NO" << endl; else { for (int i = 1 ; i<=n; i++) cout << dis[i] << " " ; } cout << endl; return 0 ; }
最长路 + SPFA
1 2 3 4 dis[nx] < dis[cur] + len dis.assign (n+1 , -INT_MAX); graph[a].emplace_back (b, c);
最短路 + Bellman-Ford
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 #include <iostream> #include <vector> #include <algorithm> #include <queue> #include <climits> using namespace std;struct edge { int x, y, l; }; vector<edge> e; vector<int > dis; int n, m;bool Bellman_Ford () dis[1 ] = 0 ; for (int i = 1 ; i<n; i++) for (int j = 1 ; j<=m; j++) dis[e[j].y] = min (dis[e[j].y], dis[e[j].x]+e[j].l); for (int i = 1 ; i<=m; i++) if (dis[e[i].x] + e[i].l < dis[e[i].y]) return false ; return true ; } int main () cin >> n >> m; e.resize (m+1 ), dis.resize (n+1 ); for (int i = 1 ; i<=m; i++) { cin >> e[i].y >> e[i].x >> e[i].l; } if (Bellman_Ford ()) for (int i = 1 ; i<=n; i++) cout << dis[i] << " " ; else cout << "NO" ; return 0 ; }
同余最短路
当出现形如「给定 n 个整数,求这 n 个整数能拼凑出多少的其他整数(n
个整数可以重复取)」,以及「给定 n 个整数,求这 n
个整数不能拼凑出的最小(最大)的整数」,或者「至少要拼几次才能拼出模 K
余 p 的数」的问题时可以使用同余最短路的方法。
同余最短路利用同余来构造一些状态,可以达到优化空间复杂度的目的。
利用同余构造的状态可以看作单源最短路中的点。同余最短路的状态转移是
算法题解🔑
深度优先搜索基础dfs basic
Description
输入一个有向图,从顶点1开始,按照标号从小到大做dfs,对边进行分类。
我们在做dfs的时候,当访问到一个节点时,会出现四种情况:
1.此节点未被访问过,则此次的访问关系边(发起点——>接受点)称为树边(tree
edge);
2.此节点被访问过但此节点的子孙还没访问完,换句话说,此次的发起点的源头可以追溯到接收点,则此次访问关系边称为后向边(back
edge);
3.此节点被访问过且此节点的子孙已经访问完,而且发起点是搜索初始边,则称为前向边(down
edge);
4.此节点被访问过且此节点的子孙已经访问完,而且发起点不是搜索初始边,则称为横叉边(cross
edge)。
Input
输入的第一行包含两个整数n和m,n是图的顶点数,m是边数。1<=n<=100,0<=m<=10000。
接下来的m行,每行是一个数对u
v,表示存在有向边(u,v)。顶点编号从1开始。
接下来的1行,包含一个整数k,表示会查询k条边的类型。
接下来的k行,每行是一个数对u v,表示查询边u v的类型。
Output
对每条查询的边,单独一行输出边的类型,参见输出样例。
Sample InputCopy
1 2 3 4 5 6 7 8 9 10 11 12 4 6 1 2 2 3 3 1 1 3 1 4 4 2 4 1 2 3 1 1 3 4 2
Sample OutputCopy
1 2 3 4 edge (1,2) is Tree Edge edge (3,1) is Back Edge edge (1,3) is Down Edge edge (4,2) is Cross Edge
答案:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 #include <iostream> #include <cstring> using namespace std;bool matrix[101 ][101 ]; bool isvisited[101 ];int edgeKind[101 ][101 ];int vers, edges;string kind[4 ] = {"Tree Edge" , "Back Edge" , "Cross Edge" , "Down Edge" }; bool isAllVisited (int v) for (int i = 1 ; i<=vers; i++) if (matrix[v][i]&&(!isvisited[i])) return false ; return true ; } void DFS (int v) for (int i = 1 ; i<=vers; i++){ if (matrix[v][i]){ if (!isvisited[i]){ isvisited[i] = 1 ; edgeKind[v][i] = 0 ; DFS (i); } else if (!isAllVisited (i)) edgeKind[v][i] = 1 ; else if (v != 1 ) edgeKind[v][i] = 2 ; else edgeKind[v][i] = 3 ; } } } int main () cin >> vers >> edges; memset (matrix, false , 101 *101 *sizeof (bool )); memset (isvisited, false , 101 * sizeof (bool )); memset (edgeKind, -1 , (vers + 1 ) * (vers + 1 ) * sizeof (int )); int a, b; for (int i = 0 ; i<edges; i++){ cin >> a >> b; matrix[a][b] = true ; } isvisited[1 ] = true ; DFS (1 ); int test; cin >> test; while (test--){ cin >> a >> b; cout << "edge (" << a << "," << b << ") is " << kind[edgeKind[a][b]] << endl; } return 0 ; }
最小生成树
力扣1584.连接所有点的最小费用
给你一个points 数组,表示 2D 平面上的一些点,其中
points[i] = [xi, yi] 。
连接点 [xi, yi] 和点 [xj, yj]
的费用为它们之间的 曼哈顿距离
:|xi - xj| + |yi - yj| ,其中 |val| 表示
val 的绝对值。
请你返回将所有点连接的最小总费用。只有任意两点之间
有且仅有 一条简单路径时,才认为所有点都已连接。
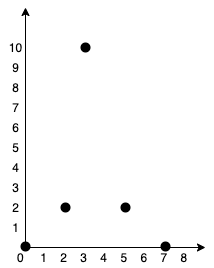
示例 1:
img
1 2 3 4 5 6 输入:points = [[0,0],[2,2],[3,10],[5,2],[7,0]] 输出:20 解释: 我们可以按照上图所示连接所有点得到最小总费用,总费用为 20 。 注意到任意两个点之间只有唯一一条路径互相到达。
示例 2:
1 2 输入:points = [[3,12],[-2,5],[-4,1]] 输出:18
示例 3:
1 2 输入:points = [[0,0],[1,1],[1,0],[-1,1]] 输出:4
示例 4:
1 2 输入:points = [[-1000000,-1000000],[1000000,1000000]] 输出:4000000
示例 5:
1 2 输入:points = [[0,0]] 输出:0
提示:
1 <= points.length <= 1000-106 <= xi, yi <= 106所有点 (xi, yi) 两两不同。
方法一:Prim 算法
随机选择一个起点,将其加入集合
遍历 lowcost,寻找 lowcost 中的最小值,假设下标为 j,则 j 为 集合V
中离集合
找到 lowcost 中的最小值 j 后,此时数组 lowcost
中的所有节点都需要更新,因此此时集合
根据新加入集合
重复步骤2,直到访问所有的节点。
image.png
绝妙的解题代码:
主要的思想是:Prim算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution {public : int minCostConnectPoints (vector<vector<int >>& points) int size = points.size (); if (size <= 1 ) return 0 ; unordered_map<int , int > dist (size) ; for (int i = 0 ; i<size; i++){ dist.emplace (i, INT_MAX); } int minnode; int minlen; int lensum = 0 ; dist[0 ] = 0 ; for (int i = 0 ; i<size; i++){ minlen = INT_MAX; for (auto & p: dist){ if (p.second < minlen){ minlen = p.second; minnode = p.first; } } lensum+=minlen; dist.erase (minnode); for (auto & p:dist){ p.second = min (p.second, (abs (points[p.first][0 ]-points[minnode][0 ])+abs (points[p.first][1 ]-points[minnode][1 ]))); } } return lensum; } };
力扣1135.最低成本连通所有城市(稀疏图)
想象一下你是个城市基建规划者,地图上有 N 座城市,它们按以 1 到 N
的次序编号。
给你一些可连接的选项 connections,其中每个选项
connections[i] = [city1, city2, cost] 表示将城市 city1
和城市 city2 连接所要的成本。(连接是双向的,也就是说城市 city1 和城市
city2 相连也同样意味着城市 city2 和城市 city1 相连)。
返回使得每对城市间都存在将它们连接在一起的连通路径(可能长度为 1
的)最小成本。
该最小成本应该是所用全部连接代价的综合。如果根据已知条件无法完成该项任务,则请你返回
-1。
示例 1:
1 2 3 4 输入:N = 3 , connections = [[1 ,2 ,5 ],[1 ,3 ,6 ],[2 ,3 ,1 ]] 输出:6 解释: 选出任意 2 条边都可以连接所有城市,我们从中选取成本最小的 2 条。
示例 2:
1 2 3 4 输入:N = 4 , connections = [[1 ,2 ,3 ],[3 ,4 ,4 ]] 输出:-1 解释: 即使连通所有的边,也无法连接所有城市。
Kruskal 算法:排序+并查集,更适合稀疏表
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 class Solution {private : vector<int > parent; int part = 0 ; int find (int a) if (parent[a] == a) return a; return find (parent[a]); } void uni (int a, int b) int pa = find (a); int pb = find (b); if (pa == pb) return ; parent[pa] = pb; part --; } public : int minimumCost (int N, vector<vector<int >>& connections) part = N; parent = vector <int >(N, 0 ); for (int i = 0 ; i < N; ++i) parent[i] = i; sort (connections.begin (), connections.end (),[](const vector<int >& a, const vector<int >& b) { return a[2 ] < b[2 ]; }); int res = 0 ; for (vector<int >& conn : connections) { int a = conn[0 ] - 1 ; int b = conn[1 ] - 1 ; int cost = conn[2 ]; int pa = find (a); int pb = find (b); if (pa != pb) { uni (a, b); res += cost; } if (part == 1 ) return res; } return -1 ; } };
Dijkstra 算法
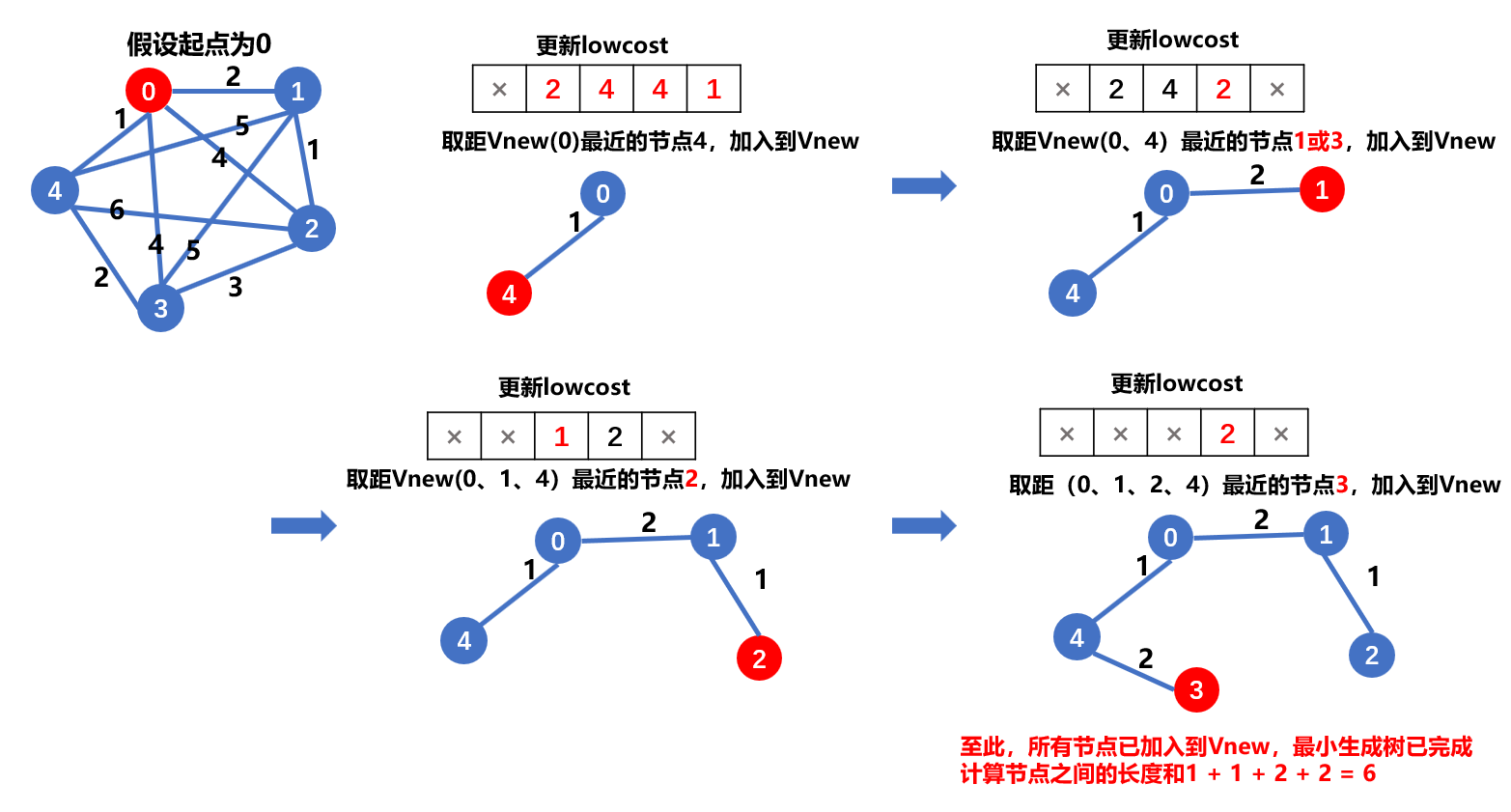
力扣1514.概率最大的路径
给你一个由 n 个节点(下标从 0
开始)组成的无向加权图,该图由一个描述边的列表组成,其中
edges[i] = [a, b] 表示连接节点 a 和 b
的一条无向边,且该边遍历成功的概率为 succProb[i] 。
指定两个节点分别作为起点 start 和终点 end
,请你找出从起点到终点成功概率最大的路径,并返回其成功概率。
如果不存在从 start 到 end 的路径,请
返回 0 。
示例 1:
img
1 2 3 输入:n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2 输出:0.25000 解释:从起点到终点有两条路径,其中一条的成功概率为 0.2 ,而另一条为 0.5 * 0.5 = 0.25
示例 2:
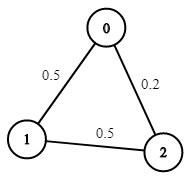
img
1 2 输入:n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2 输出:0.30000
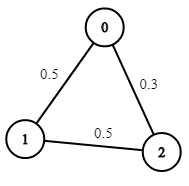
示例 3:
img
1 2 3 输入:n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2 输出:0.00000 解释:节点 0 和 节点 2 之间不存在路径
解答:
Dijkstra 算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution {public : double maxProbability (int n, vector<vector<int >>& edges, vector<double >& succProb, int start, int end) vector<vector<pair<int , double >>> graph (n); for (int i = 0 ; i<edges.size (); i++){ graph[edges[i][0 ]].emplace_back (edges[i][1 ], succProb[i]); graph[edges[i][1 ]].emplace_back (edges[i][0 ], succProb[i]); } priority_queue<pair<int ,double >> pq; vector<double > prob (n,0 ) ; prob[start] = 1 ; pq.emplace (start, 1 ); while (!pq.empty ()){ auto [v, pr] = pq.top (); pq.pop (); if (pr < prob[v]) continue ; for (auto & [node, nodepr] : graph[v]){ if (prob[node] < prob[v]*nodepr){ prob[node] = prob[v]*nodepr; pq.emplace (node, prob[node]); } } } return prob[end]; } };
SPFA算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Solution {public : double maxProbability (int n, vector<vector<int >>& edges, vector<double >& succProb, int start, int end) vector<double > dist (n, 0 ) ; vector<bool > inque (n, 0 ) ; vector<vector<pair<int , double >>> graph (n); int i = 0 ; for (auto & e: edges){ graph[e[0 ]].emplace_back (e[1 ], succProb[i]); graph[e[1 ]].emplace_back (e[0 ], succProb[i++]); } queue<int > q; q.emplace (start); dist[start] = 1 ; inque[start] = true ; while (!q.empty ()){ int curnode = q.front (); q.pop (); inque[curnode] = false ; for (auto & [node, nodepr]: graph[curnode]){ if (dist[node] < dist[curnode]* nodepr){ dist[node] = dist[curnode]*nodepr; if (!inque[node]){ inque[node] = true ; q.emplace (node); } } } } return dist[end]; } };
SPFA算法的应用:
(此题不能使用Dijkstra)
洛谷P1073最优贸易
简述:一个人在一国旅行,有n个城市,m
条路,每条路连接两个城市,一部分单向道,另一部分双向道。水晶球在n个城市价格不一样,此人想只进行一次贸易来赚差价,如果不能赚钱,则不进行贸易。此人从
1城市 出发到 n城市,可以重复经过同一个城市。
输入:第一行有正整数 n 和 m,分别表示城市数目和道路数目。 第二行 n
个整数,表示n个城市水晶球的价格 接下来 m 行,每行三个整数 x,y,z。z
表示城市x到城市y之间的单向道路,z=2表示这条道路为城市x和城市y之间的双向道路。
输出:一 个整数,表示最多能赚取的旅费。如果没有进行贸易,则输出
0。
样例:
1 2 3 4 5 6 7 8 9 10 输入: 5 5 4 3 5 6 1 1 2 1 1 4 1 2 3 2 3 5 1 4 5 2 输出: 5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 #include <iostream> #include <algorithm> #include <vector> #include <queue> #include <climits> using namespace std;int num, road;vector<int > price; void spfa (vector<vector<int >>& travel, int start, int flag, vector<int >& d) vector<bool > inque (num, false ) ; queue<int > q; q.push (start); inque[start] = true ; d[start] = price[start]; while (!q.empty ()) { int t = q.front (); q.pop (); inque[t] = false ; for (int i:travel[t]) { if ((min (d[t], price[i])<d[i] && flag) || (max (d[t], price[i])>d[i] && !flag)) { if (flag) d[i] = min (d[t], price[i]); else d[i] = max (d[t], price[i]); if (!inque[i]) { inque[i] = true ; q.emplace (i); } } } } } int main () cin >> num >> road; vector<int > dmin (num, INT_MAX) , dmax (num, 0 ) ; vector<vector<int >> ttravel (num),retravel (num); price.resize (num); for (int i = 0 ; i<num; i++) cin >> price[i]; for (int i = 0 ; i<road; i++) { int a, b, z; cin >> a >> b >> z; a--, b--; ttravel[a].push_back (b); retravel[b].push_back (a); if (z == 2 ) { ttravel[b].push_back (a); retravel[a].push_back (b); } } spfa (ttravel, 0 , 1 , dmin); spfa (retravel, num-1 , 0 , dmax); int res = 0 ; for (int i = 0 ; i<num; i++) res = max (res, dmax[i]-dmin[i]); cout << res<< endl; return 0 ; }
此题目不适合 dijkstra 算法,因为 dijkstra
算法具有累加性,而且测试样例中可能会有环,会导致 dijkstra 反复更新。
二分法+双端队列
在郊区有 N 座通信基站,P 条 双向 电缆,第 i 条电缆连接基站 Ai 和
Bi。特别地,1 号基站是通信公司的总站,N
号基站位于一座农场中。现在,农场主希望对通信线路进行升级,其中升级第 i
条电缆需要花费 Li。电话公司正在举行优惠活动。农产主可以指定一条从 1
号基站到 N 号基站的路径,并指定路径上不超过 K
条电缆,由电话公司免费提供升级服务。农场主只需要支付在该路径上剩余的电缆中,升级价格最贵的那条电缆的花费即可。求至少用多少钱可以完成升级。
输入格式
第 1 行:三个整数 N,P,K。
第 2..P+1行:第 i+1 行包含三个整数 Ai,Bi,Li。
输出格式
包含一个整数表示最少花费。
若 1 号基站与 N 号基站之间不存在路径,则输出 −1。
题目总结 :求路径的第k+1大的费用的最小值
思路 :二分法+双端队列
每次取出对头的元素,如果有就更新
边权是 1 ,从堆尾插入
边权是 0 ,从队首插入
特别地,可能会有一个元素多次入队,只需关注第一次入队即可。
广度优先搜索,假设把每一个点的每次拓展算作一步(即所有边权值为1),那么可以一直搜索,得到层数。这个层数就是这个点到root的最短路。
相当于把权作为路径长度,s 作为衡量长度的标准,找到最小的 s
使得最短路长度大于或等于k。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 #include <deque> #include <algorithm> #include <vector> #include <iostream> using namespace std;int n, p, k;vector<vector<pair<int , int >>> graph; bool check (int s) vector<int > dist (n, INT_MAX) ; vector<bool > visited (n, false ) ; deque<int > dq; dq.emplace_back (0 ); dist[0 ] = 0 ; while (!dq.empty ()){ int t = dq.front (); dq.pop_front (); if (visited[t] == true ) continue ; visited[t] = true ; for (auto p: graph[t]){ int len = p.first, nx = p.second; bool isBigger = (len > s); if (dist[nx]>dist[t] + isBigger){ dist[nx] = dist[t]+isBigger; if (isBigger) dq.emplace_back (nx); else dq.emplace_front (nx); } } } return dist[n-1 ] <= k; } int main () cin >> n >> p >> k; graph.resize (n); for (int i = 0 ; i<p; i++) { int a, b, l; cin >> a >> b >> l; a--, b--; graph[a].emplace_back (l, b); graph[b].emplace_back (l, a); } int left = 0 , right = 1e6 +1 ; int res = -1 ;X: while (left < right) { int mid = (left+right)/2 ; if (check (mid)) { res = mid; right = mid-1 ; } else left = mid+1 ; } cout << res << endl; return 0 ; }
Floyd 算法
ACWing343.排序
Floyd 算法经典应用 —— 传递闭包
传递闭包是指在一个有向图中,如果存在一条从节点 A 到节点 B
的路径,那么节点 A 和节点 B
之间就存在传递关系。传递闭包算法就是用来计算一个有向图的传递闭包的算法。
具体来说,传递闭包算法会对图中的每个节点进行遍历,对于每个节点,它会找到所有可以到达的节点,并将这些节点与该节点建立传递关系。这样,经过一次遍历后,就可以得到图的传递闭包。
传递闭包算法的应用非常广泛,例如在数据库中,可以使用传递闭包算法来计算关系型数据库中的外键约束,以及在编译器中,可以使用传递闭包算法来计算程序中的依赖关系。
给定 n 个变量和 m 个不等式。其中 n 小于等于 26,变量分别用前 n
的大写英文字母表示。
不等式之间具有传递性,即若 A>B且 B>C,则 A>C。
请从前往后遍历每对关系,每次遍历时判断:
如果能够确定全部关系且无矛盾,则结束循环,输出确定的次序;
如果发生矛盾,则结束循环,输出有矛盾;
如果循环结束时没有发生上述两种情况,则输出无定解。
输入格式
输入包含多组测试数据。
每组测试数据,第一行包含两个整数 n 和 m。
接下来 m 行,每行包含一个不等式,不等式全部为小于关系。
当输入一行 0 0 时,表示输入终止。
输出格式
每组数据输出一个占一行的结果。
结果可能为下列三种之一:
如果可以确定两两之间的关系,则输出
"Sorted sequence determined after t relations: yyy...y.",其中't'指迭代次数,'yyy...y'是指升序排列的所有变量。
如果有矛盾,则输出:
"Inconsistency found after t relations.",其中't'指迭代次数。
如果没有矛盾,且不能确定两两之间的关系,则输出
"Sorted sequence cannot be determined."。
数据范围
2≤n≤26,变量只可能为大写字母 A∼Z。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 #include <iostream> #include <string> #include <cstring> #include <algorithm> using namespace std;#define N 26 int n, m;vector<vector<bool >> graph (N, vector <bool >(N, 0 )); vector<vector<bool >> dist (N, vector <bool >(N, 0 )); vector<bool > visited (N, 0 ) ;void floyd () dist = graph; for (int k = 0 ; k < n; k++) for (int i = 0 ; i<n; i++) for (int j = 0 ; j<n; j++) { int t = (dist[i][k]&dist[k][j])|dist[i][j]; dist[i][j] = t; } } int check () for (int i = 0 ; i<n; i++) if (dist[i][i]) return 2 ; for (int i = 0 ; i<n; i++) for (int j = 0 ; j<i; j++) if (!dist[i][j] && !dist[j][i]) return 0 ; return 1 ; } char get_min () for (int i = 0 ; i<n; i++) { if (!visited[i]) { bool flag = true ; for (int j = 0 ; j<n; j++) { if (!visited[j] && dist[j][i]) { flag = false ; break ; } } if (flag) { visited[i] = true ; return 'A' +i; } } } } int main () while (cin >> n >> m, n||m) { graph.assign (N, vector <bool >(N, 0 )); int type = 0 , t; for (int i = 1 ; i<=m ; i++) { string s; cin >> s; int a = s[0 ]-'A' , b = s[2 ]-'A' ; if (!type) { graph[a][b] = 1 ; floyd (); type = check (); if (type) t = i; } } if (!type) cout << "Sorted sequence cannot be determined." << endl; else if (type == 2 ) cout << "Inconsistency found after " << t <<" relations." << endl; else { cout << "Sorted sequence determined after " << t << " relations: " ; for (int i = 0 ; i<n; i++) cout << get_min (); cout << endl; } } return 0 ; }
Floyd 算法经典应用二
给定一张无向图,求图中一个至少包含 33
个点的环,环上的节点不重复,并且环上的边的长度之和最小。该问题称为
无向图的最小环问题 。你需要输出最小环的方案
输入:第一行包含两个整数 N 和 M,表示无向图有 N 个点,M 条边。接下来
M行,每行包含三个整数 u,v,l,表示点 u 和点 v 之间有一条边,边长为
l。
输出格式:输出占一行,包含最小环的所有节点(按顺序输出),如果不存在则输出
No solution。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 #include <iostream> #include <vector> #include <algorithm> using namespace std;#define second dot #define first len int n, m, cnt;vector<vector<int >> track; vector<int > path; void dfs (int i, int j) int k = track[i][j]; if (k == -1 ) return ; dfs (i,k); path.emplace_back (k); dfs (k,j); } void getpath (int i, int j, int k) path.clear (); path.emplace_back (i); dfs (i, j); path.emplace_back (j); path.emplace_back (k); } int main () cin >> n >> m; vector<vector<int >> graph (n, vector <int >(n, INT_MAX)); for (int i = 0 ; i<n; i++) graph[i][i] = 0 ; track.resize (n), track.assign (n, vector <int >(n, -1 )); for (int i = 0 ; i<m; i++) { int a, b, c; cin >> a >> b >> c; a--, b--; graph[b][a] = graph[a][b] = min (graph[a][b], c); } vector<vector<int >> dist (graph); int res = INT_MAX; for (int k = 0 ; k<n; k++) { for (int i = 0 ; i<k; i++) { for (int j = i+1 ; j<k; j++) { if ( (long long )dist[i][j]+graph[j][k]+graph[k][i]<res) { res = dist[i][j]+graph[j][k]+graph[k][i]; getpath (i,j,k); } } } for (int i = 0 ; i<n; i++) { for (int j = 0 ; j <n; j++) { if ( dist[i][j]>(long long )dist[i][k]+dist[k][j]) { dist[i][j] = dist[i][k]+dist[k][j]; track[i][j] = k; } } } } if (res == INT_MAX) cout << "No solution" << endl; else { for (int x:path) cout << x+1 << ' ' ; cout << endl; } return 0 ; }
类Floyd算法+qmi(快速幂)
ACWing345.牛站
题目: 给定一张由 T 条边构成的
无向图 ,点的编号为 1∼1000 之间的整数。求从起点 S 到终点
E 恰好 经过 N 条边(可以重复经过)的最短路 。
输入格式:
第 1 行:包含四个整数 N,T,S,E。
第 2...T+1
行:每行包含三个整数,描述一条边的边长以及构成边的两个点的编号。
输出格式:输出一个整数,表示最短路的长度
解题思路
在快速幂的框架下做logN次类floyd算法,时间复杂度
快速幂是一种用于快速计算幂运算的算法。它的基本思想是将指数不断折半,将底数不断平方,从而快速地计算出幂运算的结果。
具体来说,假设要计算 a 的 n 次幂,可以将 n 表示为二进制形式,例如 n =
101101(二进制),则有:
其中,
快速幂算法的时间复杂度为 O(log n),比朴素的幂运算算法的时间复杂度
O(n)
要快得多。因此,在需要进行大量幂运算的场合,快速幂算法是一种非常有效的算法。
普通的Floyd算法:
1 2 3 4 for (int k=1 ;k<=n;k++) for (int i=1 ;i<=n;i++) for (int j=1 ;j<=n;j++) d[i][j]=min (d[i][j],d[i][k]+d[k][j]);
Floyd可以得到所有点对间的最短距离是因为每次都是一条边一条边的的更新
类Floyd算法
1 2 3 4 5 vector<int > temp (N, INT_MAX) ;for (int k = 0 ; k<n; k++) for (int i = 0 ; i<n; i++) for (int j = 0 ; j<n; j++) temp[i][j] = min (temp[i][j], a[i][k]+b[k][j]);
这种算法具有边的特性,因为它不会拿之前完成计算的数据进行更新,而是用单独的边之间的和进行自我更新。这保证更新时,边数的限制。
第一次拿1条边更新2条边的结果,第二次拿2条边的结果更新四条边的结果,以成倍的速度更新。
Floyd算法可以用于求解图中任意两点之间的最短路径。它的基本思想是采用动态规划的思想,利用中间节点来逐步优化路径。在Floyd算法的过程中,需要对路径进行多次更新,每次更新时需要遍历整张图。这样的时间复杂度为
假设存在一个矩阵A,表示图中节点之间的距离,初始时A的值就是图的邻接矩阵。则经过k次更新后,A的值表示的就是任意两点之间经过不超过k个节点的最短路径。也就是说,A的k次幂就是经过k个中间节点的最短路径。因此,可以通过对A进行矩阵乘法快速幂的运算,来快速得到任意两点之间的最短路径。具体步骤如下:
将图的邻接矩阵存储为一个n x n的矩阵A。
对A进行k次幂运算,得到矩阵Ak,表示经过k个中间节点的最短路径。
对于任意两个节点i和j,Ak[i][j]表示i到j的经过k个中间节点的最短路径。
取所有Ak[i][j]中的最小值,即为节点i到节点j的最短路径。
使用矩阵乘法快速幂优化Floyd算法的时间复杂度为
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 #include <iostream> #include <climits> #include <vector> #include <map> #include <algorithm> using namespace std;#define N 210 #define vv vector<vector<int> > vv modle (N, vector<int >(N, INT_MAX)) ;vv graph (modle) ; vv res (modle) ;map<int , int > id; int m, t, s, e, n;void mul (vv& c, vv a, vv b) static vv temp (modle) temp.assign (N, vector <int >(N, INT_MAX)); for (int k = 0 ; k<n; k++) { for (int i = 0 ; i<n; i++) { if (a[i][k]!=INT_MAX) for (int j = 0 ; j<n; j++) { if (b[k][j]!=INT_MAX) temp[i][j] = min (temp[i][j], a[i][k]+b[k][j]); } } } c = temp; } void qmi () for (int i = 0 ; i<n; i++) res[i][i] = 0 ; while (m) { if (m&1 ) mul (res, res, graph); mul (graph, graph, graph); m >>= 1 ; } } int main () cin >> m >> t >> s >> e; if (!id.count (s)) id[s] = n++; if (!id.count (e)) id[e] = n++; s = id[s], e = id[e]; while (t--) { int a, b, c; cin >> c >> a >> b; if (!id.count (a)) id[a] = n++; if (!id.count (b)) id[b] = n++; a = id[a], b = id[b]; graph[a][b] = graph[b][a] = min (graph[a][b], c); } qmi (); cout << res[s][e] << endl; return 0 ; }
匈牙利算法
P1129 [ZJOI2007]
矩阵游戏
题目大意 :矩阵游戏在一个
游戏目的 :通过若干次操作,使得方阵的主对角线(左上角到右下角的连线)上的格子均为黑色。
输入:第一行一个整数
T,表示数据的组数,对于每组数据,输入格式如下:
第一行为一个整数,代表方阵的大小 n,接下来 n 行,每行 n 个非 0 即 1
的整数,代表该方阵。其中,0代表白色,1 代表黑色。
输出 :对于每组数据,若关卡有解则输出
Yes,否则输出 No。
分析 :我们把矩阵转化为
二分图(左侧集合代表各行,右侧集合代表各列,某位置为 1
代表该行和该列之间有边)。进行一系列 交换操作,使得 X1 连上
Y1,X2连上Y2,...
大家可以想象,所谓的交换,是不是可以等价为
重命名 ?我们可以在保持当前二分图结构的情况下,把右侧点的编号进行改变,者与交换的效果是等价的。所以让
X1,X2...与 Y1,Y2...一一对应,其实只需要原图最大匹配数为 4就行了。
代码 :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 #include <iostream> #include <cstring> using namespace std;int Map[205 ][205 ], p[205 ], vis[205 ], N, T;bool match (int i) for (int j = 1 ; j<=N; j++) { if (Map[i][j] && !vis[j]) { vis[j] = 1 ; if (p[j] == 0 && match (p[j])) { p[j] = i; return true ; } } } return false ; } int Hungarian () int cnt = 0 ; for (int i = 1 ; i<=N; i++) { memset (vis, 0 , sizeof (vis)); if (match (i)) cnt++; } return cnt; } int main () cin >> T; while (T--) { cin >> N; memset (p, 0 , sizeof (p)); for (int i = 1 ; i<=N; i++) for (int j = 1 ; j<=N; j++) cin >> Map[i][j]; int res = Hungarian (); if (res == N) cout << "Yes" << endl; else cout << "No" << endl; } return 0 ; }
(vijos1204)CoVH之柯南开锁
题目大意 :有一个矩阵锁,由 M*N
个格子组成,其中某些格子凸起(灰色),每一次操作可以把一行格子给按下去。求把所有凸起格子按下去所需的最少次数。
输入 :第一行 两个不超过 100 的整数 N,M表示矩阵的
长和宽 以下 N 行,每行 M 个数,非 0 即 1,1表示凸起方格
输出 :一个整数,所需的最小次数
图片
把样例转化为 二分图的形式为:
按下一行其实就是删掉与某一个点相连的所有边,现在要求最少的操作次数,就相当于求
最小点覆盖数。直接用匈牙利算法即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 #include <iostream> #include <cstring> using namespace std;int matrix[102 ][102 ];int p[102 ] = {0 };int vis[102 ];int n, m;bool match (int x) for (int i = 1 ; i<=m; i++) { if (matrix[x][i] && !vis[i]) { vis[i] = true ; if (p[i] == 0 || match (p[i])) { p[i] = x; return true ; } } } return false ; } int Hungarian () int cnt = 0 ; for (int i = 1 ; i<=n; i++) { memset (vis, 0 , sizeof (vis)); if (match (i)) cnt++; } } int main () cin >> n >> m; for (int i = 1 ; i<=n; i++) for (int j = 1 ; j<=m; j++) { char c; cin >> c; matrix[i][j] = c-'0' ; } cout << Hungarian () << endl; return 0 ; }
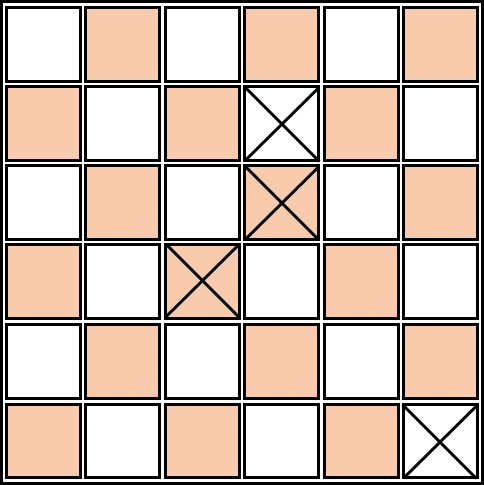
(TYVJ P1035)棋盘覆盖
题目 :给出一张 n*n(n<=100)
的国际象棋棋盘,其中被删除了一些点,问可以使用多少 1*2
的多米诺骨牌进行掩盖。
输入格式 :第一行为 n,m(表示有 m 个删除的格子)
第二行到 m+1 行为 x,y,分别表示删除格子所在的位置,x 为 第 x 行,y 为第
y 列。
输出格式 :一个数,即最大覆盖个数
把棋盘染色,每个多米诺骨牌恰好覆盖一个白格和一个黑格。
删除一些格子:
现在求多米诺骨牌最大覆盖数。
染色之后,黑格与白格可以构成一个二分图,每个白格都只与黑格相连,每个黑格也只与白格相连。在给所有黑格和白格编号后,我们把每个未删除的格子都与它上下左右紧邻的未删除的格子相连。很显然,这张二分图的最大匹配数,就是我们能放下最多多米诺骨牌数。注意,因为数据范围比较大,要用邻接表存图。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 #include <iostream> #include <vector> using namespace std;vector<bool > del; vector<vector<int >> graph; vector<int > link; vector<bool > vis; static constexpr int dirs[4 ][2 ] = {{1 , 0 }, {-1 , 0 }, {0 , 1 }, {0 , -1 }};int n, m;int idx (int x, int y) return x*n + y; } bool match (int x) for (int i: graph[x]) { if (!vis[i]) { vis[i] = true ; if (link[i] == -1 || match (p[i])) { link[i] = x; return true ; } } } return false ; } int hungarian () int cnt = 0 ; for (int i = 0 ; i<n*n; i++) { vis.assign (n*n, false ); if (match (i)) cnt++; } return cnt; } int main () cin >> n >> m; del.resize (n*n), del.assign (n*n, false ); graph.resize (n*n), vis.resize (n*n), link.resize (n*n), link.assign (n*n, -1 ); for (int i = 0 ; i<m; i++) { int dx, dy; cin >> dx >> dy; dx--, dy--; del[idx (dx, dy)] = true ; } for (int i = 0 ; i<n; i++) { for (int j = 0 ; j < n; j++ ) { if (!del[idx (i,j)]) for (int k = 0 ; k<4 ; k++) { int nx = i+dirs[k][0 ]; int ny = j+dirs[k][1 ]; if (nx>=0 && nx<n && ny>=0 && ny<n && !del[idx (nx,ny)]) { graph[idx (i,j)].emplace_back (idx (nx,ny)); } } } } cout << hungarian ()/2 << endl; return 0 ; }
同余最短路
P3403 跳楼机
题目大意 :给定 , , , , ,
分析 :首先可以将
则有
像这样建图后,
最后统计时, 对于
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 #include <iostream> #include <vector> #include <queue> #include <climits> #include <algorithm> #include <cstdio> using namespace std;vector<vector<pair<long long int ,long long int >>> graph; vector<long long int > dis; long long int h, x, y, z;void spfa () queue<long long int > q; vector<bool > inque (x, false ) ; q.emplace (1 ); dis[1 ] = 1 ; while (!q.empty ()) { long long int cur = q.front (); q.pop (); inque[cur] = false ; for (auto t: graph[cur]) { long long int nx = t.second; long long int len = t.first; if (dis[nx] > dis[cur]+len) { dis[nx] = dis[cur]+len; if (!inque[nx]) { q.emplace (nx); inque[nx] = true ; } } } } } int main () scanf ("%lld%lld%lld%lld" , &h, &x, &y, &z); if (x==1 ||y==1 ||z==1 ) { cout<< h << endl; return 0 ; } graph.resize (x+1 ), dis.resize (x+1 ),dis.assign (x+1 , LONG_LONG_MAX/2 ); for (int i = 0 ; i<x; i++) { graph[i].emplace_back (y, (i+y)%x); graph[i].emplace_back (z, (i+z)%x); } spfa (); long long int ans = 0 ; for (int i = 0 ; i<x; i++) { if (dis[i]<=h) ans += (h-dis[i])/x + 1 ; } printf ("%lld\n" , ans); return 0 ; }
(ARC84B
Small Multiple )
题目大意:给一个k,对于所有k的倍数,求这些数中十进制下各位和的最小值。
1 2 3 4 5 6 7 8 9 10 11 12 for (int i = 1 ; i<k; i++){ if (i != (i+1 )%k) graph[i].emplace_back (1 , (i+1 )%k); if (i != (10 *i)%k) graph[i].emplace_back (0 , (10 *i)%k); } cout << 1 +dis[0 ]; dis[1 ] = 0 ; q.emplace (1 );