图论Tarjan算法

卡布叻_米菲 Lv2
  2023-04-10 13:05 2023-04-10 13:05 创建   2024-02-08 13:09:12 2024-02-08 13:09:12 更新      

Tarjan 算法是图论中非常实用 / 常用的算法之一，能解决 强连通分量，双连通分量，割点和桥，求 最近公共祖先（LCA）等问题。

Tarjan 算法是基于 深度优先搜索DFS 的算法，用于求解 图的连通性问题。Tarjan 算法可以在线性时间求出 无向图的割点与桥，进一步求解 无向图的双连通分量；同时，也可以求解 有向图的强连通分量、必经点与必经边。

无向图的割点与桥

如果删除无向图中的某个点会使无向图的连通分量数增多，则把这个点称为割点。类似地，如果删除无向图中的某条边会使无向图的连通分量数增多，则把这个点称为割边或桥。割点与桥可以用Tarjan算法求出。

img

img

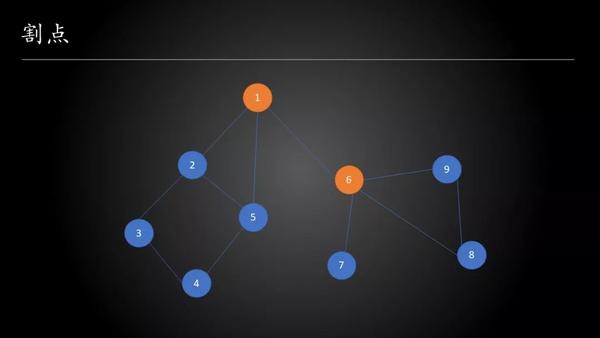
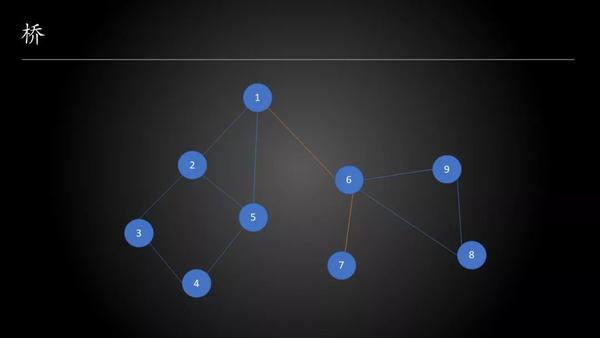
桥

Tarjan 算法在求解无向图的割点与桥的工作原理

时间戳：时间戳是用来标记图中每个节点在进行深度优先搜索时被访问的时间顺序（相当于一个序号，这个序号由小到大），用 dfn[x] 来表示

搜索树：在无向图中，我们以某一个节点 x 出发进行深度优先搜索，每个节点只访问一次，所有被访问过的节点与边构成一棵树，我们可以称之为“无向连通图的搜索树”。

追溯值：追溯值 用来表示 从当前节点x 作为搜索树的根节点出发，能够访问到的所有节点中，时间戳最小的值 —— low[x]。

"能够访问到的所有节点" 满足①以 x 为根的搜索树的所有节点②通过一条非搜索树上的边能够到达搜索树的所有结点 这两点中的一点即可。

断言：如果 p 是 q 的父节点，并且 low(q)>dfsn(p)，那么 p↔︎q 是桥。如果 p↔︎q 不是桥，那么删掉这条边后一定有其他路径可以到达p。注意无向图没有横叉边，想要到达p只能通过子树反向边实现，那么low(q)≤dfsn(p)应该成立，然而这与条件矛盾。因此 p↔︎q 是桥。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
vector<pair<int, int>> bridges;
int dfsn[MAXN], low[MAXN], fa[MAXN], cnt;
void tarjan(int p)
{
    low[p] = dfsn[p] = ++cnt;
    for(auto to: edges[p])
    {
        if(!dfsn[to])
        {
            fa[to] = p; //记录父节点
            tarjan(to);
            low[p] = min(low[p], low[to]);
            if(low[to] > dfs[p])
            	bridges.emplace_back(p, to);
		}
        else if(fa[p] != to) //排除父节点
        	low[p] = min(low[p], dfsn[to]);
    }
}

割点问题

设 low(u) 表示 u 所在子树中的节点经过至多一条非树边所能到达的节点中最小 dfs 序。

如果 p 存在一个子节点q满足 low(q)≥dfsn(p)，说明 q 无法通过它的子树 “逃”到比 p 的dfs序更小的节点。那么，既然走子树走不通，q 如果想要达到这样的点，只能选择经过它的父节点 p。因此如果删去 p，q 的 dfs 序小于 p 点的点就分开了。

这时我们一般可以说 p 是割点了，只有一种特殊情况，就是 p 是dfs生成树的根节点的情形。这时，整个连通分量都不存在比 p 的dfs序更小的点。对于根节点，它如果有两个以上子节点，那么它就是割点（显然删除根节点后这两个分支将会互不相连）。

在实现时，不再需要像强连通分量一样维护一个栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int dfsn[MAXN], low[MAXN], cnt;
vector<int> cut; //存储所有的割点
void tarjan(int p, bool root = true)
{
    int tot = 0;
    low[p] = dfsn[p] = ++cnt;
    for(auto q: edges[p])
    {
        if(!dfsn[q])
        {
            tarjan(q, false);
            low[p] = min(low[p], low[q]);
            tot += (low[q]>=dfsn[p]);// 统计满足low[q] >= dfsn[p]的子节点数目
        }
        else 
            low[p] = min(low[p], dfsn[q]);
    }
    if(tot > root)
        cut.push_back(p);
}

强连通分量

对于一张有向图而言，它是强连通的当且仅当其上 每个顶点都相互可达。强连通图类似于嵌套的环，强连通图一定有环，但 n 个节点的强连通图不一定有n元环。

img

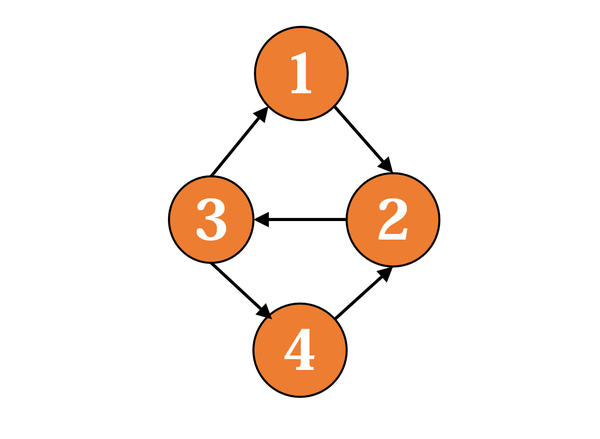
强连通分量 是 有向图的极大的强连通子图，所谓“极大”意味着，把图划分为若干个强连通分量后，不存在两个强连通分量相互可达。

处理 强连通分量 的一个有力的工具是 dfs 生成树。在dfs时，每当通过某条边 e 访问到一个新节点v，就加入这个点和这条边，最后得到的便是 dfs 生成树。例如对于下面这张有向图：

img

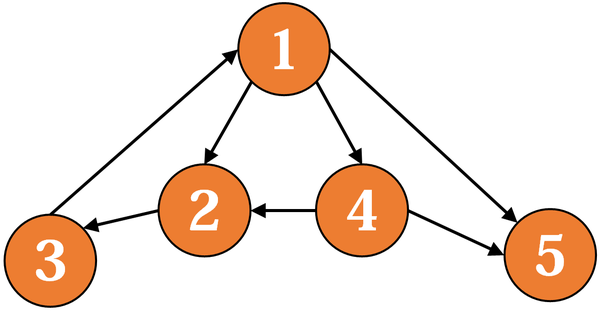
它的 dfs 生成树可能时这样的（黑色实线）：

img

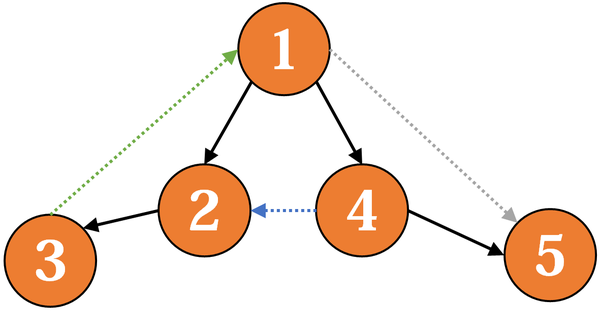
除了生成树的树边外，原图剩下的边可以分为三种：

  • 前向边（灰色虚线）：从某个点到它的某个子孙节点的边。这种边相当于提供某种“捷径”，在这个问题里不太重要，即使把它们删除对于连通性也没什么影响。
  • 反向边（绿色虚线）：从某个点到它的某个祖先节点的边。这种边就是产生环的原因，如果删去所有的反向边，那么原图就会成为无环图。
  • 横叉边（蓝色虚线）：从某个点到一个既非它子孙节点，也非它祖先节点的边。这种边本身不会产生环，但是它可能把两个强连通子图连接起来，形成一个更大的强连通图。

反向边 和 横叉边 都有一个特点：起点的dfs序 必然大于 终点的dfs序。

结论：对于每个强连通分量，存在一个点是其他所有点的祖先。若不然，则可以把强连通分量划成 n 个分支，使各分支的祖先节点互相不为彼此的祖先，这些分支间不能通过树边相连，只能通过至少 n 条横叉边相连，但这必然违背上一段的性质。

img

我们把这个唯一的祖先节点称为强连通分量的根。显然，根是强连通分量中dfs序最小的节点。

为了求强连通分量，我们常常使用 Tarjan 算法。首先，我们把 low(p) 定义为 p 所在子树的节点经过最多一条非树边 u→v（其中 v 可达 u）能到达的节点中最小的 dfs序。根据这样的定义，某个点 p 是强连通分量的根，等价于 dfsn(p) = low(p)。我们这里必须强调 v 可达 u，否则会使 low(5)=2，但它实际应是一个强连通分量的根。

img

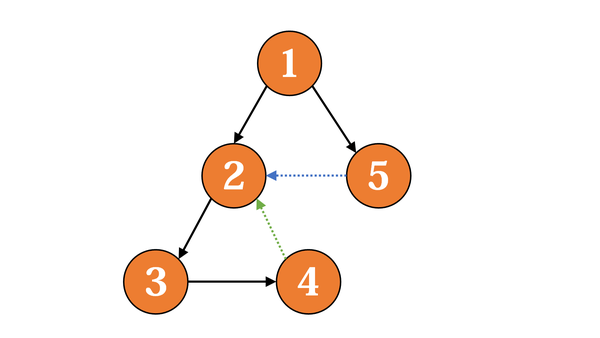
low(p) 可以通过动态规划得到，对于以某个点p为起点的边 p→q：

  • 如果 q 从未访问过，则 q 在 p 所在的子树上，如果某节点 r 从 q 起可以经过最多一条反向边到达，则从 p 起也可以（先从 p 到 q，再到 r），于是先递归处理点 q，然后令 low(p) = min(low(p), low(q))。
  • 如果 q 已访问过，且从 q 可以到达 p，令 low(p) = min(low(p), dfsn(q))。
  • 如果 q 已经访问过，且从 q 不能到达 p，不做处理。（后两种情况都是非树边）

但是我们怎么确认一个点能不能到达另一个点呢？因为 反向边 和 横向边 都是指向dfs序较小的节点，而 前向边 的存在又不影响状态转移方程，所以我们只需要确认 比该点dfs序小 的哪些点能到达该点即可，这可以用一个 栈 动态地维护。

每当搜索到新店，就令它入栈。在对 p 的搜索结束时，如果 low(p) = n<dfsn(q)，设dfs序为n的点为q，则 p 点到达 q点都可达，考虑对 q 点的搜索很可能没有结束，所以 p 应该留在栈中。如果发现 p 满足low(p) = dfsn(p)，则说明 p 是某个强连通分量的根，它和栈中的子孙相互可达。但同时，它可栈中子孙点也无法到达 p 的祖先节点，以及祖先节点其他尚未搜索的分支，所以不断从栈顶弹出元素，知道弹出p（注意这样维护的栈中的dfs序是单调增的），同时记录答案。

举例：（这里为了方便，直接用dfs序作为点的编号）

img

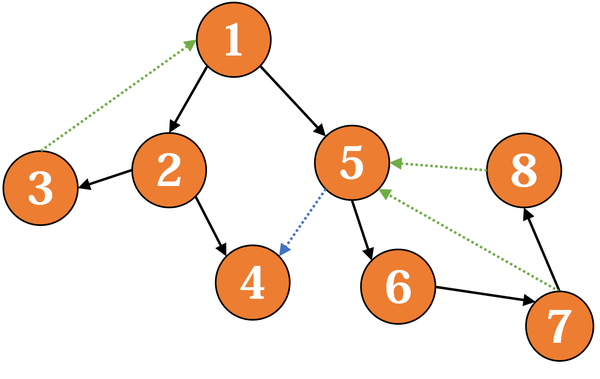
沿着 1 → 2 → 3 搜索（节点右上角表示当前的 low，下方为栈）：

img

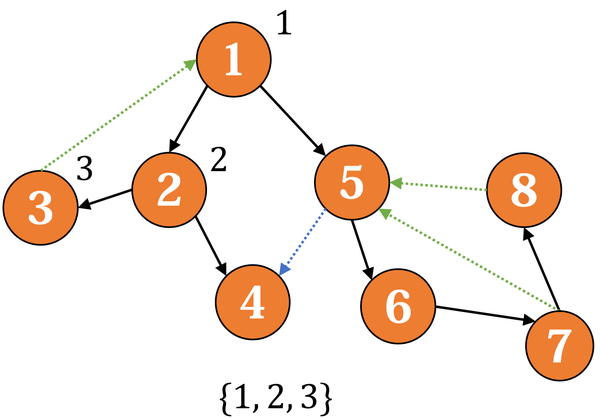
发现反向边 3 → 1，更新 low(3)，然后回到2搜索4：

img

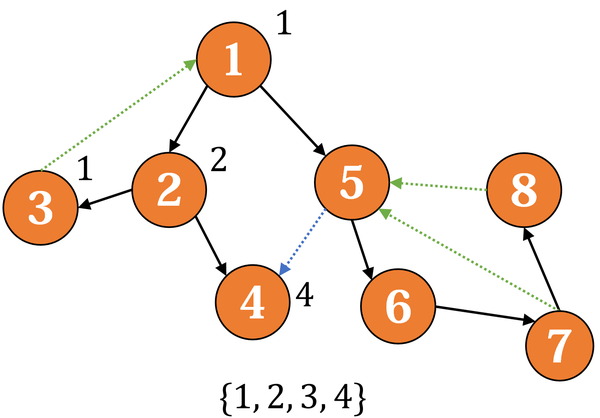
4没有出边，返回，这时发现 low(4) = dfsn(4) = 4，于是出栈，标记它属于第一个强连通分量。

img

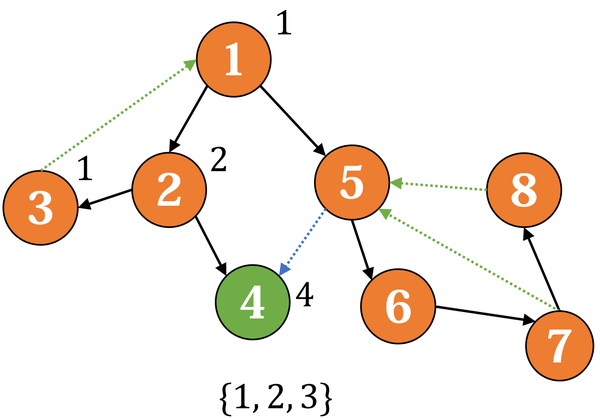
回到2，它对应的子树已搜索完毕，更新 low(2)；接下来搜索 5 → 6 → 7 → 8：

img

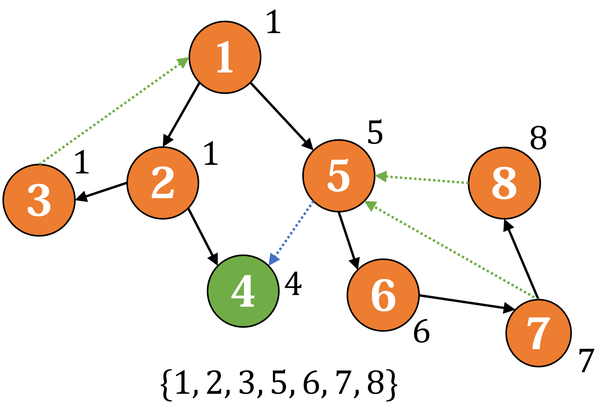
反顺序更新它们的 low，到5发现 low(5) = dfsn(5) = 5，于是把它放入新的强连通分量：

img

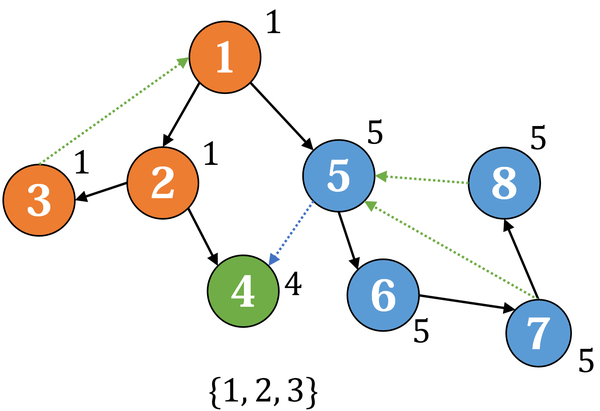
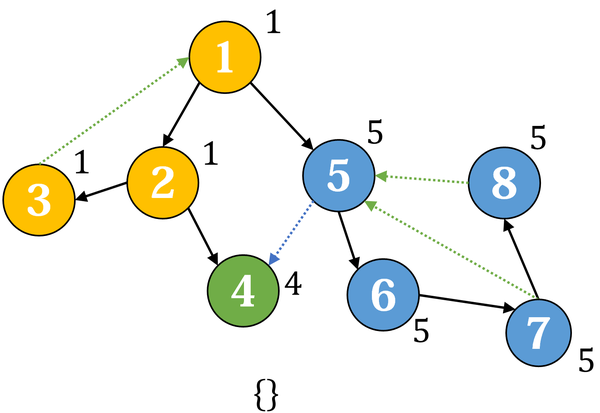
最后回到1 ，把剩下还在栈内的节点都归入最后一个强连通分量：

img

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
stack<int> stk;
// instk：是否在栈中  scc：每个点所属的强连通分量编号  cscc：强连通分量的数量
int dfsn[MAXN], low[MAXN], instk[MAXN], scc[MAXN], cnt, cscc;
void tarjan(int p)
{
    low[p] = dsfn[p] = ++cnt;
    instk[p] = 1;
    stk.push(p);//入栈
    for(auto q: edges[p])
    {
        if(!dfsn[q]) //未访问过
        {
            tarjan(q); //递归搜索
            low[p] = min(low[p], low[q]);
		}
        else if(instk[q]) //访问过
        	low[p] = min(low[p], dfsn[q]);
    }
    if(low[p] == dfsn[p]) //发现强连通分量的根
    {
        int top;
        cscc++;
        do
        {
            top = stk.top();
            stk.pop();
            instk[top] = 0;
            scc[top] = cscc;
        }while(top != p) //知道弹出p才停止
	}
}

注意，由于原图并不一定是强连通图，所以不能随便找一个点作为根dfs就完事，而要保证每个点都被dfs到：

1
2
3
for (int i = 1; i <= n; ++i)
    if (!dfsn[i])
        tarjan(i);

由于每次dfs结束后，栈都已清空，所以各次dfs并不会互相影响。

在求出强连通分量后，可以进行 缩点，即：把处于同一强连通分量的点当作同一个点处理。这样，我们可以得到一张 有向无环图。此外。注意到编号较小的点不能到达编号较大的点，于是scc编号的顺序还符合拓扑序（编号越大的点拓扑序越靠前）。

1
2
3
4
for(int u = 1; u<=n; u++)
    for(auto v: edges[u])
        if(scc[u] != scc[v])
            edges2[scc[u]].push_back(scc[v]);

例如，在有向图中求经过的点权值之和最大的路径，就可以缩点，每个点的权值为缩之前的点的权值之和，这是因为如果一条路径经过强连通分量中的某个点，就可以经过其中的所有点。对于缩点后得到的有向无环图，可以按照拓扑序DP。

再例如，求有向图中那些所有点都可达的点，也可以缩点，因为如果 p 可达 q ，那么 p 所在的强连通分量中的所有点都可达 q 。对于得到的有向无环图，只需找到唯一的出度为0的点即可。

模板题

缩点

题目描述

给定一个 个点 条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。

允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。

输入格式

第一行两个正整数

第二行 个整数，其中第 个数 表示点 的点权。

第三至 行，每行两个整数 ，表示一条 的有向边。

输出格式

共一行，最大的点权之和。

样例输入

1
2
3
4
2 2
1 1
1 2
2 1

样例输出

1
2

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
#include<iostream>
#include<vector>
#include<queue>
#include<stack>
#include<algorithm>
using namespace std;

int n, m;
vector<vector<int>> graph, newgraph; //原来的点图 和 缩点后的图
vector<int> dfsn, low, scc, indeg, weight, newwgt, dist;
//dfsn 追溯的时间戳， low 最小时间戳， scc 每个点的强连通集合的下标
//indeg 每个强连通集合的入度，weight 每个点的权值，newwgt 每个强连通集合权值
//dist 每条路径的最大权值
vector<bool> instk; //是否在栈中
stack<int> stk;//栈
int tot = 0, cscc = 0;
//tot 遍历时候所经过的点数，cscc强连通集合的个数
void tarjan(int x)
{
	instk[x] = true;
	dfsn[x] = low[x] = ++tot;
	stk.emplace(x);//放入栈中
	
	for(int nx: graph[x])
	{
		if(!dfsn[nx]) //没有访问过 
		{
			tarjan(nx);
			low[x] = min(low[x], low[nx]);
		}
		else if(instk[nx]) //访问过且在栈中 
		{
			low[x] = min(low[x], dfsn[nx]);
		}
	}
	
	if(dfsn[x] == low[x]) //特判 根起点 
	{
		int top;
		cscc++;
		do{
			top = stk.top();
			stk.pop();
			instk[top] = false;
			scc[top] = cscc; //记录每个点对应的此时的强连通集合下标
		}while(top != x); //知道弹出 x 为止 
	}
}

int main()
{
	cin >> n >> m;
	graph.resize(n+1), dfsn.resize(n+1), dist.resize(n+1), low.resize(n+1), scc.resize(n+1), instk.resize(n+1), weight.resize(n+1);
	instk.assign(n+1, false), dfsn.assign(n+1, 0), dist.assign(n+1, 0);
	
	for(int i = 1; i<=n; i++)
	{
		cin >> weight[i];
	}
	int a, b;
	for(int i = 1; i<=m; i++)  //构建有向图 
	{
		cin >> a >> b;
		graph[a].emplace_back(b);
	}
	//经典遍历操作
	for(int i = 1; i<=n; i++)
	{
		if(!dfsn[i]) //若没有访问此节点
			tarjan(i);
	}
	
	//缩点 
	newgraph.resize(cscc+1), indeg.resize(cscc+1), newwgt.resize(cscc+1);
	indeg.assign(cscc+1, 0), newwgt.assign(cscc+1, 0);
	//缩点建图
	for(int i = 1; i<=n; i++)
	{
		for(auto nx: graph[i])//遍历该点连接的所有点
		{
			if(scc[i] != scc[nx]) //如果不在同一个集合，将两个集合连接在一起
			{
				newgraph[scc[i]].emplace_back(scc[nx]); //建新图 
				indeg[scc[nx]]++; //入度 
			}
		}
		newwgt[scc[i]] += weight[i]; //整合集合的权值
	}
	
    //类似 拓扑排序 
	queue<int> q;
	for(int i = 1; i<=cscc; i++)
	{
		if(indeg[i] == 0) //入度为 0，入队
		{
			q.emplace(i);
			dist[i] = newwgt[i];
		}
	}
	
	while(!q.empty())
	{
		int cur = q.front();
		q.pop();
		
		for(auto nx: newgraph[cur])
		{
			dist[nx] = max(dist[nx], dist[cur]+newwgt[nx]);
			indeg[nx]--;
			if(indeg[nx] == 0) //拓扑排序
			{
				q.emplace(nx); 
			}
		}
	}
	
	int ans = 0;
	for(auto i: dist)
	{
		ans = max(ans, i);
	}
	
	cout << ans << endl;
	return 0;
}

割点

题目描述

给出一个 个点， 条边的无向图，求图的割点。

输入格式

第一行输入两个正整数 。

下面 行每行输入两个正整数 表示 到 有一条边。

输出格式

第一行输出割点个数。

第二行按照节点编号从小到大输出节点，用空格隔开。

样例输入

1
2
3
4
5
6
7
8
6 7
1 2
1 3
1 4
2 5
3 5
4 5
5 6

样例输出

1
2
1 
5

解题注意点

判断割点：

  • 其为根，有至少两个子树，则其为割点

    对这种割点，显然这两个子树只有根这一条路。在遍历时，只有为被访问过的儿子才会有 child 加一

  • 若 cur 不是根，但是 low[nx] > dfsn[cur]，则其为割点。

    假设遍历到 cur，low[nx] > dfsn[cur] 表示儿子 nx 点回溯可到达的最先点的时间戳大于等于 cur 的时间戳，证明不能通过 cur 以外的点与 已知点相连，那么意味着必然可以通过割去 cur 而使得已遍历点与儿子 nx 位于两个互不连通的图。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include<iostream>
#include<vector>
#include<queue>
#include<stack>
#include<algorithm>
using namespace std;

vector<vector<int>> graph;
vector<int> dfsn, low;
vector<bool> instk, ans;
stack<int> stk;
int n, m, root, tot = 0, cnt = 0;

void tarjan(int cur)
{
	dfsn[cur] = low[cur] = ++tot;
	int son = 0;
	for(int nx: graph[cur])
	{
		if(!dfsn[nx])
		{
			son++;
			tarjan(nx);
			low[cur] = min(low[cur], low[nx]);
			if(low[nx] >= dfsn[cur] && cur != root) //第二种割点
			{
				cnt += !ans[cur];
				ans[cur] = true;
			}
		}
		else
		{
			low[cur] = min(low[cur], dfsn[nx]);
		}
	}
	
	if(son >= 2 && cur == root) //第一种割点
	{
		cnt += !ans[cur];
		ans[cur] = true;
	}
}

int main()
{
	cin >> n >> m;
	graph.resize(n+1), dfsn.resize(n+1), low.resize(n+1), ans.resize(n+1), instk.resize(n+1);
	dfsn.assign(n+1, 0), low.assign(n+1, 0), instk.assign(n+1, false), ans.assign(n+1, false);
	
	while(m--)
	{
		int a, b;
		cin >> a >> b;
		graph[a].emplace_back(b);
		graph[b].emplace_back(a);
	}
	
	for(int i = 1; i<=n; i++)
	{
		if(!dfsn[i])
		{
			root = i;
			tarjan(i);
		}
	}
	
	cout << cnt << endl;
	for(int i = 1; i<=n; i++)
	{
		if(ans[i]) cout << i << " ";
	}
	cout << endl;
	return 0;
}

例题

tarjan算法与无向图连通性

ACWing363.B城

题目描述 B 城有 n 个城镇，m 条双向道路。每条道路连结两个不同的城镇，没有重复的道路，所有城镇连通。把城镇看作节点，把道路看作边，容易发现，整个城市构成了一个无向图。

输入格式：第一行包含两个整数 n 和 m。接下来 m 行，每行包含两个整数 a 和 b，表示城镇 a 和 b 之间存在一条道路。

输出格式：输出共 n 行，每行输出一个整数。第 i 行输出的整数表示把与节点 i 关联的所有边去掉以后（不去掉节点 i 本身），无向图有多少个有序点 (x,y)，满足 x 和 y 不连通。

分析

很容易让人想到 Tarjan 求割点。如果一个点不是割点，那么将它删去后其他点仍然连通，只有这个点与其它点都不连通。注意到题目要求的是有序数对，故答案为 2(n−1)。

如果一个点是割点，那么将它删去后会有三种连通块：

  1. 以满足时间戳大于等于当前节点（即割点判断标准）的子节点为代表的子树。
  2. 当前节点本身。
  3. 由除了上述两种连通块之外的所有节点构成的连通块。

对于一个大小为 p 的连通块，它对答案的贡献为 p×(n-p)。我们可以在执行 Tarjan 算法时顺便统计子树大小和这些信息即可。

tarjan算法与有向图连通性

ACWing367.学校网络

问题：一些学校连接在一个计算机网络上，学校之间存在软件支援协议，每个学校都有它应支援的学校名单（学校 A 支援学校 B，并不表示学校 B 一定要支援学校 A）。

当某校获得一个新软件时，无论是直接获得还是通过网络获得，该校都应立即将这个软件通过网络传送给它应支援的学校。因此，一个新软件若想让所有学校都能使用，只需将其提供给一些学校即可。现在请问最少需要将一个新软件直接提供给多少个学校，才能使软件能够通过网络被传送到所有学校？最少需要添加几条新的支援关系，使得将一个新软件提供给任何一个学校，其他所有学校就都可以通过网络获得该软件？

输入格式 第 1 行包含整数 N，表示学校数量。 第 2 ... N+1 行，每行包含一个或多个整数，第 i+1 行表示学校 i 应该支援的学校名单，每行最后都有一个 0 表示名单结束（只有一个 0 即表示该学校没有需要支援的学校）。

输出格式 输出两个问题的结果，每个结果占一行。

问题分析

Tarjan 缩点将原图转化为 有向无环图(DAG)，统计每个强连通分量的出度和入度，起点数量为 src，中点数量为 des。对于一个强连通分量，其中只要有一所学校获得新软件那么整个分量都能获得。

问题一：

结论：只要把软件给所有起点即可，答案为起点个数 src

证明：所有起点都无法由别的点到达，因此每个起点必须分配一个软件，而对于其他所有点一定存在前驱，一定能由某个起点到达。总结而言，从起点出发能遍历整个图。

问题二：

结论：若scc_cnt = 1（只有一个强连通分类），则不需要连新的边，答案为0。若scc_cnt>1，则答案为 max(src, des)。

证明：设缩点后的 有向无环图，起点（入度为0）的集合为P，终点（出度为0）的集合为Q。分以下两种情况讨论：

  1. |P|≤|Q|

    ①若 |P| = 1，则只有一个起点，并且这个起点能走到所有点，只要将每个终点都向这个起点连一条边，那么对于图中任意一点，都可以到达所有点，新加边的数量为|Q|

    ②若 |P|≥2，则|Q|≥|P|≥2，此时至少存在2个起点p1，p2，2个终点q1，q2，满足p1能走到q1，p2能走到q2。此时，我们可以从q1向p2新连一条边，那么此时起点和终点的个数都会减少一个，只要以这种方式，连接新边|P|-1条，则|P'|=1，而|Q'|=|Q|-(|P|-1)，由①得，再连接|Q'|条新边，那么总添加的新边数量为 |P|-1+|Q|-(|P|-1)=|Q|。

  2. |Q|≤|P|，情况与1对称，此时答案为 |P|。

综上所述，scc_cnt > 1 时，问题二的答案为 max(|P|, |Q|)，即 max(src, des)。

  • 标题: 图论Tarjan算法
  • 作者: 卡布叻_米菲
  • 创建于 : 2023-04-10 13:05:00
  • 更新于 : 2024-02-08 13:09:12
  • 链接: https://carolinebaby.github.io/2023/04/10/tarjan算法/
  • 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
评论
此页目录
图论Tarjan算法
  1. 无向图的割点与桥
    1. 桥
    2. 割点问题
  2. 强连通分量
  3. 模板题
    1. 缩点
    2. 割点
  4. 例题