算法中的数学

算法学习过程中积累数学知识真的很重要，可以极大地优化算法。

content: 快速幂，极角排序，凸包

[TOC]

位运算

常用的位运算：

• 获取一个数二进制的某一位

  // 获取 a 的第 b 位，最低编号为 0 
  int getBit(int a, int b)
  {
      return (a >> b)&1;
  }

• 将一个数二进制的某一位设置为 0

  //将 a 的第 b 位设置为 0，最低位编号为 0
  int unsetBit(int a, int b)
  {
      return a & ~(1 << b);
  }

• 将一个数二进制的某一位设置为 1

  //将 a 的第 b 位设置为 1，最低位编号为 0
  int setBit(int a, int b)
  {
      return a|(1<<b);
  }

• 将一个数二进制的某一位取反

  //将 a 的第 b 位取反，最低编号为 0
  int flapBit(int a, int b)
  {
      return a^(1<<b);
  }

汉明权重

汉明权重 是一串符号中不同于零符号的个数。对于一个 二进制数，它的汉明权重就等于它 1 的个数

求一个汉明权值可以循环求解：不断去掉这个数在二进制下的最后一位（即 右移一位），维护一个答案变量，在除的过程中根据最低位是否为 1 更新答案。

//求 x 的汉明权重
int popcount(int x)
{
    int cnt = 0;
    while(x)
    {
        cnt += x&1;
        x >>= 1;
    }
    return cnt;
}

求一个数的汉明权值 还可以用 lowbit （一个数二进制表示从低往高的第一个 1 连同后面的零，如 的 lowbit 是 ）：不断减去它的 lowbit，知道这个数为 0

int popcount(int x)
{
    int cnt = 0;
    while(x)
    {
        cnt++;
        x -= x & -x; 
    }
    return cnt;
}

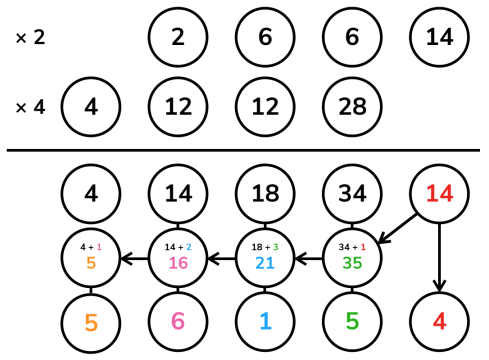
构造汉明权重递增的排列

在 状压dp 中，按照 popcount 递增的顺序枚举 有时可以避免重复枚举状态。这是构造汉明权重递增排列的一大作用。

在 O(n) 时间内构造 汉明权重递增的排列

我们知道，一个汉明权重为 n 的最小的整数为 。只要可以在常数时间构造出一个整数汉明权重相等的后继，我们就可以通过枚举汉明权重，从 开始不断寻找下一个数的方式，在 时间内构造出 的符合要求的排列。

而找出一个数 x 汉明权重相等的后继有这样的思路，以 为例：

• 把 最右边的 1 向左移动，如果不能移动，移动它左边的 1，以此类推，得到

• 将第一步得到的数的最后移动的 1 原先的位置一直到最低位的所有 1 都移到最右边。

  1. 找到第一步中移动的最后一个 1 的位置，即从右往左数第 k 位。
  2. 将第 k 位及其右边的所有 1 移到最右边，同时将第 k−1 位变成 1。
  3. 将第 k−1位及其右边的所有 1 移到最右边，同时将第 k−2 位变成 1。
  4. 重复上述步骤，直到所有从右往左数的 1 都移到了最右边。

  以 为例，第一步得到的数是 ，最后移动的 1 原来在第三位，所以将最后三位 010 移到最右边，得到 。

算法优化：

int t = x + (x & -x);
x = t | ((((t&-t)/(x&-x))>>1)-1);

• 第一个步骤中，我们把数 x 加上它的 lowbit，在二进制表示下，就相当于把 x 的最右边的连续一段 1 换成它左边的一个 1。如刚才提到的 二进制数，它在加上它的 lowbit 后是 。这其实得到了我们答案的前半部分。
• 我们接下来要把答案后面的 1 补齐，t 的 lowbit 是 x 最右边连续一段 1 最左边 1 移动后的位置，而 x 的 lowbit 则是 x 最右边连续一段 1 最左边的位置。还是以 为例，t = ，，。
• 接下来的除法操作，最关键。 我们设原数最右边连续一段 1 最高位的 1 在第 r 位上（位数从 0 开始），最低位的 1 在第 ​ 位，t 的 lowbit 等于 1 << (r+1) ，x 的 lowbit 等于 1 << l， (((t&-t)/(x&-x))>>1)得到的，就是 (1<<(r+1))/(1<<l)/2 = (1<<r)/(1<<l) = 1<<(r-l) ，在二进制表示下就是 1 后面跟上 个零，零的个数正好等于连续 1 的个数减去 1 。举我们刚才的数为例，。把这个数减去 1 得到的就是我们要补全的低位，或上原来的数就可以得到答案。

所以枚举 按汉明权重递增的排列的完整代码为：

for(int i = 0; (1 << i)-1 <= n; i++)
{
    for(int x = (1 << i)-1, t; x<=n; 
        t = x+(x&-x), x = x? (t|((((t&-t)/(x&-x))>>1)-1)) : (n+1))
    {
        //...需要完成的操作
    }
}

其中要注意 0 的特判，因为 0 没有相同汉明权重的后继。

高精度计算

高精度计算（Arbitrary-Precision Arithmetic），也被称作 大整数（bignum）计算，运用了一些算法结构来支持更大整数间的运算（数字大小超过语言内建整型）

背景

输入：一个形如 a <op> b 的表达式。

• a、b 分别是长度不超过 1000 的十进制非负整数；
• <op> 是一个字符（+、-、* 或 /），表示运算。
• 整数与运算符之间由一个空格分隔。

输出：运算结果。

• 对于 +、-、* 运算，输出一行表示结果；
• 对于 / 运算，输出两行分别表示商和余数。
• 保证结果均为非负整数。

在平常的实现中，高精度数字利用字符串表示，每一个字符表示数字的一个十进制位。因此可以说，高精度数值计算 实际上是一种特别的 字符串处理。

读入字符串时，数字最高位在字符串首（下标小的位置）。但是习惯上，下标最小的位置存放的是数字的 最低位，即存储反转的字符串。这么做的原因在于，数字的长度可能发生变化，同时希望同样权值位始终保持对齐（例如，希望所有的个位都在下标 [0]，所有的十位都在下标 [1]...）；同时，加、减、乘的运算一般都从个位开始进行（回想小学的竖式运算～），这都给了「反转存储」以充分的理由。

读入高精度数字的代码：

void clear(int a[])
{
    for(int i = 0; i<LEN; i++)
        a[i] = 0;
}

void read(int a[])
{
    static char s[LEN+1];
    scanf("%s", s);
    
    clear(a);
    int len = strlen(s);
    //反转存储
    for(int i = 0; i<len; i++) a[len-i-1] = s[i] - '0'; //字符对应的数字大小
}

输出也按照逆序输出。如果不想输出前导0，故从最高位向下寻找第一个非零位。

void print(int a[])
{
    int i;
    for(i = LEN-1; i >= 1; i--)
        if(a[i] != 0) break;
    for(; i>=0; i--) putchar(a[i]+'0');
    putchar('\n');
}

四则运算

加法：高精度加法就是竖式加法。从最低位开始，将两个加数对应位置上的数码相加，并判断是否大于或等于 10。如果达到 那就进位，并使该位数-10。

void add(int a[], int b[], int c[]) 
{
  clear(c);
  for (int i = 0; i < LEN - 1; ++i) 
  {
    c[i] += a[i] + b[i]; // 将相应位上的数码相加
    if (c[i] >= 10) // 进位
    {
      c[i + 1] += 1;
      c[i] -= 10;
    }
  }
}

减法：竖式减法

void sub(int a[], int b[], int c[]) 
{
  clear(c);
  for (int i = 0; i < LEN - 1; ++i) 
  {
    c[i] += a[i] - b[i]; // 逐位相减
    if (c[i] < 0) 
    {
      c[i + 1] -= 1;    // 借位
      c[i] += 10;
    }
  }
}

乘法：

• 高精度—单精度

  一个直观的思路是直接将 a 每一位上的数字乘以 b。之后从个位开始逐位向上处理进位。但是这里的进位可能非常大，甚至远大于 9，因为每一位被乘上之后都可能达到 9b 的数量级。所以这里的进位不能再简单地进行 -10 运算，而是要通过除以 10 的商以及余数计算。当然，也是出于这个原因，这个方法需要特别关注乘数 b 的范围。若它和 （或相应整型的取值上界）属于同一数量级，那么需要慎用高精度—单精度乘法。

  void mul_short(int a[], int b, int c[]) 
  {
    clear(c);
    for (int i = 0; i < LEN - 1; ++i) 
    {
      c[i] += a[i] * b;    // 直接把 a 的第 i 位数码乘以乘数，加入结果
      if (c[i] >= 10)      // 处理进位
      {
        c[i + 1] += c[i] / 10; //即除法的商数成为进位的增量值
        c[i] %= 10; //即除法的余数成为在当前位留下的值
      }
    }
  }

• 高精度—高精度

  竖式乘法。竖式乘法的每一步，实际上是计算了若干 的和。例如计算 ，计算的就是 。

  

  于是可以将 b 分解为它的所有数码，其中每个数码都是单精度数，将它们分别与 a 相乘，再向左移动到各自的位置上相加即得答案。当然，最后也需要用与上例相同的方式处理进位。

  注意这个过程与竖式乘法不尽相同，我们的算法在每一步乘的过程中并不进位，而是将所有的结果保留在对应的位置上，到最后再统一处理进位，但这不会影响结果。

  void mul(int a[], int b[], int c[]) 
  {
    clear(c);
  
    for (int i = 0; i < LEN - 1; ++i) 
    { // 这里直接计算结果中的从低到高第 i 位，且一并处理了进位
    // 第 i 次循环为 c[i] 加上了所有满足 p + q = i 的 a[p] 与 b[q] 的乘积之和
   // 这样做的效果和直接进行上图的运算最后求和是一样的，只是更加简短的一种实现方式
      for (int j = 0; j <= i; ++j) c[i] += a[j] * b[i - j];
      if (c[i] >= 10) 
      {
        c[i + 1] += c[i] / 10;
        c[i] %= 10;
      }
    }
  }

除法：竖式除法

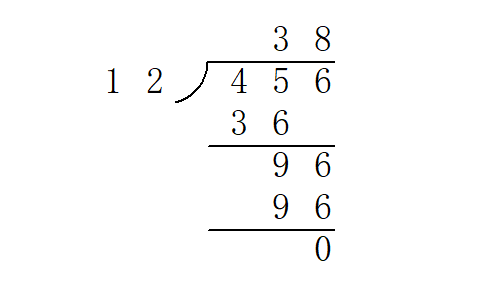
竖式长除法实际上可以看作一个逐次减法的过程。例如上图中商数十位的计算可以这样理解：将 45 减去三次 12 后变得小于 12，不能再减，故此位为 3。

为了减少冗余运算，我们提前得到被除数的长度 与除数的长度 ，从下标 开始，从高位到低位来计算商。这和手工计算时将第一次乘法的最高位与被除数最高位对齐的做法是一样的。

下面程序实现了一个函数 greater_eq() 用于判断被除数以下标 last_dg 为最低位，是否可以再减去除数而保持非负。此后对于商的每一位，不断调用 greater_eq()，并在成立的时候用高精度减法从余数中减去除数，也即模拟了竖式除法的过程。

// 被除数 a 以下标 last_dg 为最低位，是否可以再减去除数 b 而保持非负
// len 是除数 b 的长度，避免反复计算
inline bool greater_eq(int a[], int b[], int last_dg, int len) 
{
  // 有可能被除数剩余的部分比除数长，这个情况下最多多出 1 位，故如此判断即可
  if (a[last_dg + len] != 0) return true;
  // 从高位到低位，逐位比较
  for (int i = len - 1; i >= 0; --i) 
  {
    if (a[last_dg + i] > b[i]) return true;
    if (a[last_dg + i] < b[i]) return false;
  }
  // 相等的情形下也是可行的
  return true;
}

void div(int a[], int b[], int c[], int d[]) 
{
  clear(c);
  clear(d);

  int la, lb;
  for (la = LEN - 1; la > 0; --la)
    if (a[la - 1] != 0) break;
  for (lb = LEN - 1; lb > 0; --lb)
    if (b[lb - 1] != 0) break;
  if (lb == 0) 
  {
    puts("> <");
    return;
  }  // 除数不能为零

  // c 是商
  // d 是被除数的剩余部分，算法结束后自然成为余数
  for (int i = 0; i < la; ++i) d[i] = a[i];
  for (int i = la - lb; i >= 0; --i) 
  {
    // 计算商的第 i 位
    while (greater_eq(d, b, i, lb)) 
    {
      // 若可以减，则减
      // 这一段是一个高精度减法
      for (int j = 0; j < lb; ++j) 
      {
        d[i + j] -= b[j];
        if (d[i + j] < 0) 
        {
          d[i + j + 1] -= 1;
          d[i + j] += 10;
        }
      }
      // 使商的这一位增加 1
      c[i] += 1;
      // 返回循环开头，重新检查
    }
  }
}

快速幂

快速幂（平方求幂）是一种简单有效的小算法，它可以以 O(logn) 的时间复杂度来计算乘方。

前言

让我们先来思考一个问题：7的10次方，怎样算比较快？

方法1：最朴素的想法，7*7=49，49*7=343，... 一步一步算，共进行了9次乘法。

这样算无疑太慢了，尤其对计算机的CPU而言，每次运算只乘上一个个位数，无疑太屈才了。这时我们想到，也许可以拆分问题。

方法2：先算7的5次方，即7*7*7*7*7，再算它的平方，共进行了5次乘法。

但这并不是最优解，因为对于“7的5次方”，我们仍然可以拆分问题。

方法3：先算7*7得49，则7的5次方为49*49*7，再算它的平方，共进行了4次乘法。

模仿这样的过程，我们得到一个在 O(log n) 时间内计算出幂的算法，也就是快速幂。

递归快速求幂

方法三用到的就是二分的思路，由此可以得到一个递归方程：

计算 a 的 n 次方，如果 n 是偶数（不为0），那么先计算 a 的 n/2 次方，然后平方；如果n是奇数，那么先计算a的n-1次方，再乘上a；递归出口时 a 的0次方为 1。

//递归快速求幂
int qpow(int a, int n)
{
    if(n == 0)
        return 1;
    else if(n%2 == 1)
        return qpow(a, n-1)*a;
    else
    {
        int temp = qpow(a, n/2); 
        return temp*temp;
    }
}

第10行的temp变量十分重要，否则写成 qpow(a, n/2)*qpow(a,n/2) 会导致算法退化为 O(n)。

在实际问题中，题目通常会要求对一个大数取模，这是因为计算结果可能非常大。在快速幂也应当进行取模，但是要注意：要步步取模，如果MOD较大，应开 long long

//递归快速求幂(同时取模)
long long int qpow(long long int a,long long  int n)
{
    if(n == 0)
        return 1;
    else if(n%2 == 1)
        return qpow(a, n-1)*a % MOD;
    else
    {
        int temp = qpow(a, n/2); 
        return temp*temp%MOD;
    }
}

若将递归改写成循环，可以避免对栈空间的大量占用。

非递归快速幂

对于 ，这次我们选择把 10 写成 二进制形式 。

现在我们要计算 ，将它差分为 ，。实际上，对于任意的整数，我们都可以拆成若干 的形式相乘。而这些 ，恰好就是 ，，，...我们只需要把底数的平方就可以算出它们。

//非递归快速幂
int qpow(int a, int n) 
{
    int ans = 1;
    while(n)
    {
        if(n&1)      //如果 n 的当前末位为 1
            ans*=a;  //ans 乘上当前的 a
        a*=a;        //a自乘
        n>>=1;       //n往右移一位
    }
    return ans;
}

快速幂拓展

在算 时，只要 a 的数据类型支持 乘法 且满足结合律，快速幂 的算法都是有效的。

矩阵、高精度整数，都可以按照快速幂的思路计算。

代码模板：

//泛型非递归快速幂
template <typename T>
T qpow(T a, long long n)
{
    T ans = 1;
    while(n)
    {
        if(n&1)
            ans = ans*a; //最好不要用自乘，自乘需要重载*=
        n>>=1;
        a = a*a;
    }
    return ans;
}

较复杂的快速幂的时间复杂度与它与底数相乘的时间复杂度有关。

例题

斐波那契数列有以下性质 请求出 的值

分析

设矩阵 ，我们有 ，于是：

这个问题可以转化为矩阵幂的问题，这就可以应用 快速幂进行求解

#include<cstdio>
#define MOD 10e9+7
typedef long long ll;
struct matrix
{
    ll a1, a2, b1, b2;
    matrix(ll a1, ll a2, ll b1, ll b2) : a1(a1), a2(a2), b1(b1), b2(b2) {}
    matrix operator*(const matrix& y)
    {
        matrix ans((a1 * y.a1 + a2 * y.b1) % MOD,
                   (a1 * y.a2 + a2 * y.b2) % MOD,
                   (b1 * y.a1 + b2 * y.b1) % MOD,
                   (b1 * y.a2 + b2 * y.b2) % MOD);
        return ans;
    }
};
matrix qpow(matrix a, ll n)
{
    matrix ans(1, 0, 0, 1); //单位矩阵
    while (n)
    {
        if (n & 1)
            ans = ans * a;
        a = a * a;
        n >>= 1;
    }
    return ans;
}

int main()
{
    ll x;
    matrix M(0, 1, 1, 1);
    scanf("%lld", &x);
    matrix ans = qpow(M, x - 1);
    printf("%lld\n", (ans.a1 + ans.a2) % MOD);
    return 0;
}

博弈论

IGG博弈

所讨论的博弈问题满足以下条件：

• 玩家只有两个人，轮流做出决策
• 游戏的状态集有限，保证游戏在有限步后结束，这样必然会产生不能操作者
• 对任何一种局面，胜负只决定于局面本身，而与哪位选手无关

取石子游戏：组合数学领域的经典问题，基本上都是两个玩家，轮流抓石子，胜利的标准式抓走最后的石子。

玩家设定：先取石子的是玩家A（先手A），后取石子的是玩家B（后手B）。

三种经典玩法：

• 巴什博奕(Bash Game)
• 尼姆博奕(Nimm Game)
• 威佐夫博奕(Wythoff Game)

（一）巴什博弈

设定条件：1 堆石子 每次最多取m个、至少取 1 个

分析：

CASE 1：如果 n = m+1，那么由于一次最多只能取 m 个，所以，无论先取者拿走多少个，后取者都能都拿走剩余的物品，后者取胜。

CASE 2：n = (m+1)*r+s（r 为 任意自然数，s ≤ m），那么 先取者 要拿走 s 个物品，如果后者拿走 k（1 ≤ k ≤ m）个，那么先取者再拿走 m+1-k 个，结果剩下 (m+1)(r-1) 个，以后保持这样的取法，那么先取者肯定获胜。

CASE 3：n = r*(m+1) ，先手拿走 k（1 ≤ k ≤ m）个，那么后手再拿走 m+1-k 个，结果剩下(m+1)(r-1)个，以后这样保持，则后手胜。

总之，要保持给对手留下 （m+1）的倍数，就能获胜。

（m+1）的局面为 奇异局势

（二）尼姆博弈

设定条件：有 n 堆石子，每堆石子的数量是 a1, a2, a3, ......，两人 一次从这些石子堆中的任意一个取任意的石子，至少 1 个，最后一个拿光石子的人胜利。

分析

n = 1：先手全拿，先手必胜

n = 2：有两种情况，一种可能相同，一种情况比另一堆少（多）

• (m, m) 按照 “有一学一” 的方式，先手取多少个，后手取多少个，最终，后手必赢。
• (m, M) 先手先从 多的一堆中拿出 (M-m) 个，此时后手面对 (m,m) 的局势，先手必赢。

n = 3：

• (m, m, M) 先手可以先拿 M，之后变成 (m, m, 0) 的局面，按照上述做法，先手必赢。
• (a1, a2, a3) ，先手必败局为：a1, a2, a3 异或的结果为 0。其他情况有 先手赢的可能性。

...

最终的结论：

所有数 异或为 0， 先手必败，否则 有赢的可能。

例题：Nim 游戏

给定 n 堆石子，两位玩家轮流操作，每次操作可以从任意一堆石子拿走任意数量的石子（至少一个），最后无法操作的人视为失败。两人均采用最优策略，先手是否必胜。

输入： 第一行整数 n，第二行：n 个数字，其中第 i 个数字表示第 i 堆石子的数量。

输出：先手必胜，"YES"，否则，"NO"。

#include<iostream>
using namespace std;
int main()
{
    int n;
   	cin >> n;
    int a[n];
    for(int i = 0; i<n; i++) cin >> a[i];
    int ans = a[0];
    for(int i = 1; i<n; i++) ans^=a[i];
    if(ans == 0) cout << "NO" << endl;
    else cout << "YES" << endl;
    return 0;
}

（三）威佐夫博弈

设定条件：有两堆各若干个物品，两个人轮流从任一堆取至少一个或同时从两堆中取同样多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

当局势是 (1, 2)，先手有四种取法，无论先手怎么取，后手都能赢。因此 (1, 2) 是奇异局势。

哪些是奇异局势呢？

• 第一种（0，0）
• 第二种（1，2）
• 第三种（3，5）
• 第四种 (4 ，7）
• 第五种（6，10）
• 第六种 (8，13）
  
• 第七种 (9 ，15）
• 第八种 (11 ，18）
• 第n种（a，b）

规律：**a=(b-a)*1.618向下取整**

也就是：a = (int)((b-a)*1.618)这里的int是强制类型转换，注意这不是简单的四舍五入，假如后面的值是3.9，转换以后得到的不是4而是3，也就是说强制int类型转换得到的是不大于这个数值的最大整数。

有些题目要求精度较高，我们可以用下述式子来表示这个值:1.618 = (sqrt(5.0) + 1) / 2

#include<iostream>
#include<cmath>
using namespace std;
int main
{
    int a, b;
    while(cin >> a >> b)
    {
        double flag = (sqrt(5.0)+1)/2.0;
        if(a > b) swap(a,b);
        if(a == (int)((b-a)*flag)) cout << "A fail" << endl;
        else cout << "A win" << endl;
	}
    
    return 0;
}

高斯消元

输入一个包含 n 个方程 n 个未知数 的 线性方程组，方程组中的系数为实数，求解这个方程。

输入格式：第一行包含整数 n。接下来 n 行，每行包含 n+1 个实数，表示一个方程 的 n 个系数以及等号右侧的常数。

输出格式：若给定方程组存在唯一解，则输出共有 n 行，其中第 i 行输出第 i 个未知数的解，结果保留两位小数。若存在无数解，则输出Infinite group solutions。若无解，则输出 No solution。

1. 枚举第 j 列：

2. 1. 从第 k 行开始，往下找一个非0数

   2. 1. 如果没找到：

      2. 1. 输出无解

      3. 如果找到了，设它在第 k 行：

      4. 1. 交换第 j 行和第 k 行
         2. 第 j 行除以 ，使 =1
         3. 消掉第 j 列的其他元素

3. 剩下的第 n+1 列即为答案。

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
#define N 110
const double eps = 1e-8;
int n;
double a[N][N];
int gauss() // 高斯消元，答案存于 a[i][n] 中，0 <= 1 <= n
{
    int col = 0, row = 0;
    for(; col < n; col++ ) //枚举每一列
    {
        int t = row; //存绝对值最大的行
        for(int i = row; i<n; i++) //找到绝对值最大的一行
            if(fabs(a[i][col]) > fabs(a[t][col])) t = i;
        if(fabs(a[t][col]) < eps) //最大值为 0
            continue;
        
        for(int i = col; i<=n; i++)//将绝对值最大的行交换到最顶端
            swap(a[t][i], a[row][i]);
        for(int i = n; i>=col; i--) //将当前行的首位变成 1
            a[row][i] /= a[row][col];
        
        for(int i = row+1; i<n; i++)
            if(fabs(a[i][col]) > eps)
                for(int j = n; j>=col; j--)
                    a[i][j] -= a[row][j]*a[i][col];
        row++;
	}
    
    if(row < n)
    {
        for(int i = row; i<n; i++)
            if(fabs(a[i][n]) > eps) return 2; //无解
        return 1; //多解
	}
    
    for(int i = n-1; i>=0; i--)
        for(int j = i+1; j<n; j++)
            a[i][n] -= a[i][j]*a[j][n];
    return 0;
}
int main()
{
    cin >> n;
    for(int i = 0; i<n; i++)
        for(int j = 0; j<=n; j++)
            cin >> a[i][j];
    int t = gauss();
    if(t == 2) cout << "No solution" << endl;
    else if(t == 1) cout << "Infinite group solutions" <<endl;//多解
    else
    {
        for(int i = 0; i<n; i++)
        {
            if(fabs(a[i][n]) < eps) a[i][n] = 0;
            printf("%.2lf\n", a[i][n]);
		}
	}
}

拓展欧几里得算法

裴蜀定理：有任意一对正整数a、b，一定存在非零整数 x、y，使得 ，且gcd(a,b)是a、b添加系数后凑出来的最小正整数。

拓展欧几里得算法 是为了算出这样的一组x，y。

采用递归思路求解：

当 b == 0 时，任何数与 0 的最大公约数都是它本身，一组解为 x = 1, y = 0。

其他情况一直递归：int d = exgcd(b, a%b, y, x)。我们就有了这个式子：gcd(a,b) = gcd(b*y + a%b*x)，而 a%b = a - a/b*b

d = b*y + a*x - a/b*x = a*x + b(y-a/b*x) 即 y = y-a/b*x ，x = x。

函数代码

int exgcd(int a, int b, int &x, int &y)
{
    if(!b)
    {
        x = 1, y = 0;
        return a;
	}
    
    int d = exgcd(b, a%b, y, x);
    y -= a/b*x;
    return d;
}

例题

给定 a, b, m，求出 x，使得其满足 a*x = b（mod m），有解输出符合条件的 x，若无解则输出 impossible。

分析：上式等价于 a*x = y*m+b ，即a*x-y*m = b

#include<iostream>
using namespace std;
int exgcd(int a, int b, int& x, int& y)
{
    if(!b)
    {
        x = 1, y = 0;
        return a;
    }
    
    int d = exgcd(b, a%b, y, x);
    y -= a/b*x;
    return d;
}
int main()
{
    int a, b, m;
    cin >> a >> b >> m;
    int x, y;
    int d = exgcd(a, m, x, y); //求出 a, b 的最大公约数
    if( b%d != 0) //即 b 不是 gcd(a, b) 的倍数
        cout << "impossible" << endl;
    else cout << (long long) x*(b/d)%m << endl;
}

极角排序

极角排序：平面上有若干点，选一点作为极点，那么每个点都有极坐标 (ρ, θ)，将它们关于极角θ排序。进行极角排序有两种方法。

第一种 直接计算极角，极坐标和直角坐标转换公式中有 ，所以可以用 来计算。然而， 的值域只有 ，而且当 时无定义，所以需要复杂的分类讨论。所幸，<cmath>中有一个 atan2(y,x) 函数，可以直接计算(x,y)的极角，值域为(-π, π]，所以可以直接使用，只不过要留心 第四象限的极角会比第一象限小。

下面是原点和极点重合的情况。对于选定的极点，对它到每个点的向量进行极角排序即可。

using Points = vector<Point>;
double theta(auto p) { return atan2(p.y, p.x);}
void psort(Points &ps, Point c = 0)
{
    sort(ps.begin(), ps.end(), [&](auto p1, auto p2){
        return lt(theta(p1-c), theta(p2-c));
    });
}

如果想减少常数，可以提前算出每个点的极角。

第二种 叉乘，叉乘的正负遵循右手定则，按旋转方向弯曲右手四指，则若拇指向上叉乘为正，拇指向下为负。也就是说，如果一个向量通过劣角旋转到另一个向量的方向需要按逆时针方向，那么叉乘为正，否则叉乘为负。

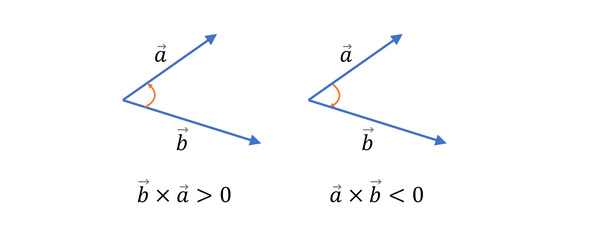
仅依靠叉乘是不能进行排序的，因为它不符合偏序关系的条件。如果定义 则 ，那么就会发现通过在坐标轴上旋转，一个向量的极角最终会小于自己。但是在同一象限内计算叉乘是可以的，所以要 先比较象限再作叉乘。

int qua(auto p) { return lt(p.y, 0) << 1 | lt(p.x, 0) ^ lt(p.y, 0); }    // 求象限
void psort(Points &ps, Point c = O)                               // 极角排序
{
    sort(ps.begin(), ps.end(), [&](auto v1, auto v2) {
        return qua(v1 - c) < qua(v2 - c) || qua(v1 - c) == qua(v2 - c) && lt(cross(v1 - c, v2 - c), 0);
    });
}

这种方法常数可能稍微大一点，但是精度比较好，如果坐标都是整数的话是完全没有精度损失的。

凸包

平面上给定若干点，则 凸包 被定义为所 能包含所有点的 凸多边形的交集。

在一切包含所有凸多边形中，凸包的面积是最小的，周长也是最小的。同时，凸包的每个顶点都是原有的点。

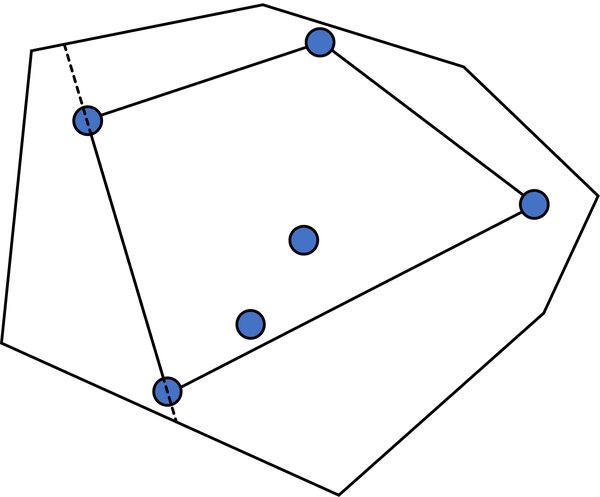
求凸包的方法有很多，包括 Graham 扫描法 和 Andrew 算法

Graham 扫描法

首先，容易发现，最左下角的一个点（这里指以横坐标为第一关键词、纵坐标为第二关键词排序后最小的点）是必然在凸包上的。我们以这个点为极点进行极角排序。显然，将极角排序后的点依次相连即可得到一个包围所有点的多边形。但是这个多边形不一定是凸的，我们需要进行调整。

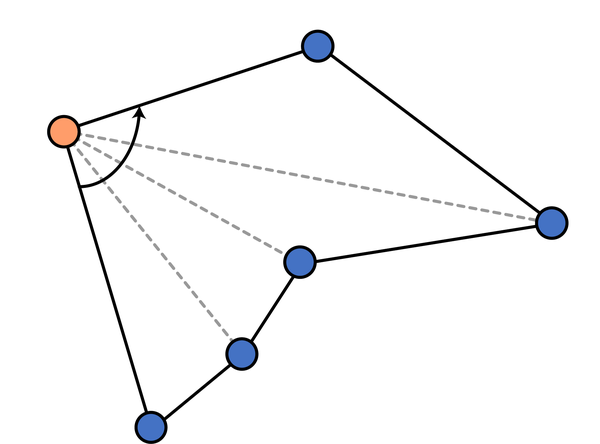
首先维护一个 栈，按照极角排序后遍历每个点，如果栈中点数小于3，就直接进栈；否则，检查栈顶三个点组成的向量的旋转方向是否为 逆时针（可用叉乘判断），若是则进栈，若不是则弹出栈顶，直到栈中点数小于3 或者满足 逆时针 条件位置。

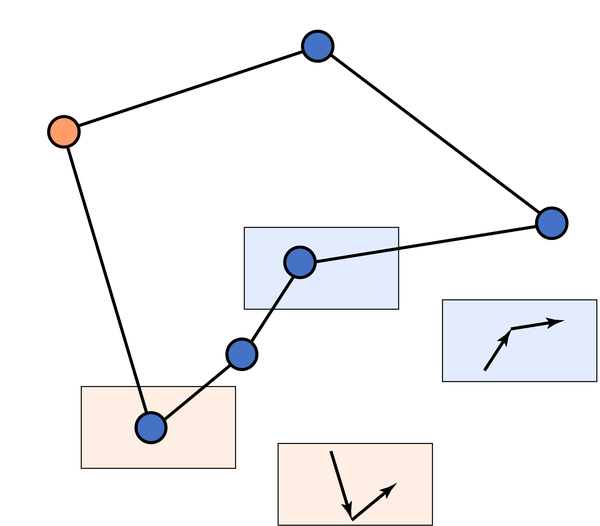
弹出栈顶的过程，相当于把三角形的两边用第三遍代替，同时又能保证包含原来的顶点。

具体过程：

实现时需要注意，要对极角排序的极点特殊处理，使它始终排在第一位。

//DEPENDS eq, lt, cross, V-V, P<P
using Points = vector<Point>;
double theta(Point p){return p==0? -1/0. : atan2(p.y, p.x);} //求极角
void psort(Points &ps, Point c) //极角排序
{
    sort(ps.begin(), ps.end(), [&](auto p1, auto p2){
        return lt(theta(p1-c), theta(p2-c));
    });
}

bool check(Point p, Point q, Point r) //检查三个点组成的两个向量旋转方向是否为逆时针
{
    return lt(0, cross(q-p, r-q));
}
Points chull(Points &ps)//以左下角的点为极角排序
{
    psort(ps, *min_element(ps.begin(), ps.end())); //以最左下角的点为极角排序
    Points H{ps[0]};
    for(int i = 0; i<ps.size(); i++)
    {
        while(H.size()>1 && check(H[H.size()-2], H.back(), ps[i]))
            H.pop_back();
        H.push_back(ps[i]);
    }
    return H;
}

Andrew 算法

另一种做法是不做极角排序，直接以横坐标为第一关键词，纵坐标为第二关键词，这样，将顶点依次相连（不首位相连）的话，也能保证不交叉。

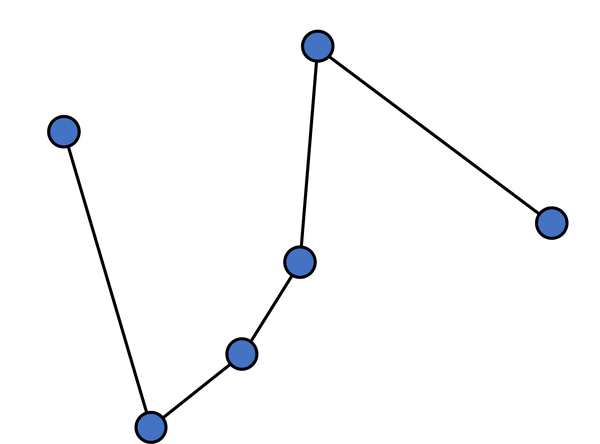
按照这样的排序顺序，像刚刚那样调整，可以求得 下凸包。

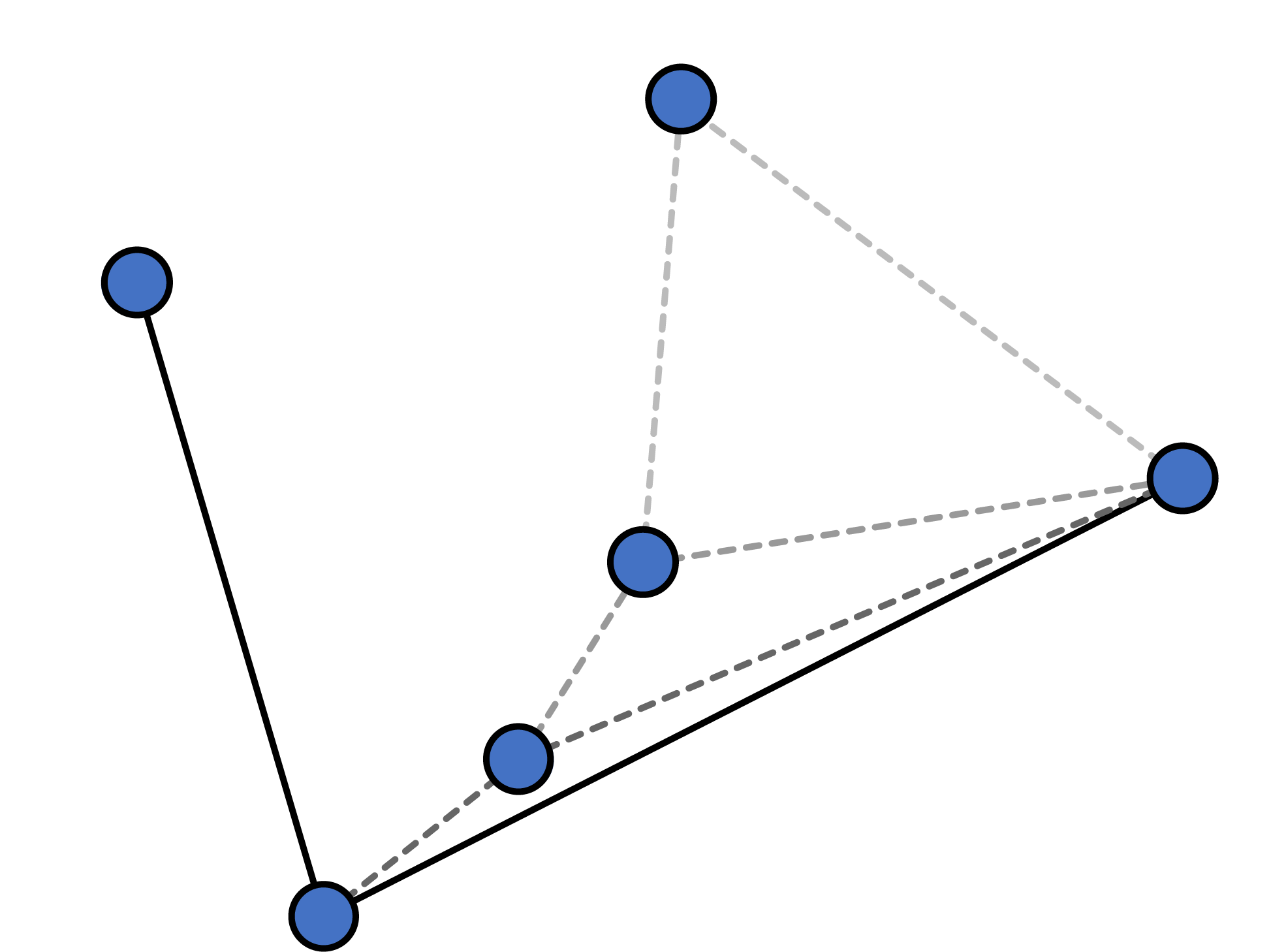
然后，再倒过来走一遍，则可以得到上凸包，两者组合即可得要求的凸包。

需要注意的是，不要把起点当作已经走过的点跳过，这样才能保证最后能够回到起点的同时保持凸包性质。但这样会使得起点会被放进两次，最后稍微处理一下即可。

//DEPENDS eq, lt, cross, V-V, P<P
using Points = vector<Point>;
bool check(Point p, Point q, Point r)
{
    return lt(0, cross(q-p, r-q));
}
Points chull(Points& ps)
{
    sort(ps.begin(), ps.end());
    vector<int> I{0}, used(ps.size());
    for(int i = 1; i<ps.size(); i++)
    {
        while(I.size()>1 && ！check(ps[I[I.size()-2]], ps[I.back()], ps[i]))
            used[I.back()] = 0, I.pop_back();
        used[i] = 1, I.push_back(i);
	}
    for(int i = ps.size()-2; i>=0; i--)
    {
        if(used[i]) continue;
        while(I.size()>1 && ！check(ps[I[I.size()-2]], ps[I.back()], ps[i]))
            I.pop_back();
        I.push_back(i);
    }
    Points H;
    for(int i = 0; i< I.size()-1; i++)
        H.push_back(ps[I[i]]);
    return H;
}

这个算法一般比前一种快一点。