算法基础

卡布叻_米菲 Lv2
  2023-04-11 22:50 2023-04-11 22:50 创建   2024-02-08 11:44:32 2024-02-08 11:44:32 更新      

content: 排序（计算排序、快速排序），前缀和，差分

1 排序

1.1 计数排序

计数排序是一种线性时间的排序算法。工作原理是使用一个额外的数组 C，其中第 i 个元素是待排数组 A 中值等于 i 的元素的个数，然后根据 数组C来将A中的元素排到正确的位置。

分为三个步骤：

  1. 计算每个数出现几次
  2. 求出每个数出现次数的前缀和
  3. 利用出现次数的前缀和，从右至左计算每个数的排名。

代码实现

1
2
3
4
5
6
7
8
9
10
const int N = 100010;
const int W = 100010;
int n, w, a[N], cnt[N], b[N];

void counting_sort(){
    memset(cnt, 0, sizeof(cnt));
    for(int i = 1; i<=n; i++) ++cnt[a[i]];
    for(int i = 1; i<=w; i++) cnt[i]+=cnt[i-1];
    for(int i = n; i>=1; i--) b[cnt[a[i]]--] = a[i];
}

1.2 基数排序

基数排序是一种非比较型的排序算法。基数排序将待排序的元素拆分为 k 个关键字，逐一对各个关键字排序后完成对所有元素的排序。

如果从第 1 个关键字到第 k 个关键字顺序进行比较，则称为 MSD基数排序

如果从第 k 个关键字到第 1 个关键字顺序进行比较，则称为 LSD基数排序

1.3 快速排序

快速排序的工作原理是通过 分治 的方式来将一个数组排序。

快速排序分为三个过程：

  1. 将数列划分为两部分（要求保证相对大小关系）；
  2. 递归到两个子序列中分别进行快速排序；
  3. 不用合并，因为此时数列已经完全有序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
struct Range {
  int start, end;

  Range(int s = 0, int e = 0) { start = s, end = e; }
};

template <typename T>
void quick_sort(T arr[], const int len) {
  if (len <= 0) return;
  Range r[len];
  int p = 0;
  r[p++] = Range(0, len - 1);
  while (p) {
    Range range = r[--p];
    if (range.start >= range.end) continue;
    T mid = arr[range.end];
    int left = range.start, right = range.end - 1;
    while (left < right) {
      while (arr[left] < mid && left < right) left++;
      while (arr[right] >= mid && left < right) right--;
      std::swap(arr[left], arr[right]);
    }
    if (arr[left] >= arr[range.end])
      std::swap(arr[left], arr[range.end]);
    else
      left++;
    r[p++] = Range(range.start, left - 1);
    r[p++] = Range(left + 1, range.end);
  }
}

我们需要对朴素快速排序思想加以优化。较为常见的优化思路有以下三种。

  • 通过 三数取中（即选取第一个、最后一个以及中间的元素中的中位数） 的方法来选择两个子序列的分界元素（即比较基准）。这样可以避免极端数据（如升序序列或降序序列）带来的退化；
  • 当序列较短时，使用 插入排序 的效率更高；
  • 每趟排序后，将与分界元素相等的元素聚集在分界元素周围，这样可以避免极端数据（如序列中大部分元素都相等）带来的退化。

下面列举了几种较为成熟的快速排序优化方式。

三路快速排序

三路快速排序 是快速排序和 基数排序 的混合。与原始的快速排序不同，三路快速排序在随机选取分界点 m 后，将待排数列划分为三个部分：小于 m、等于 m 以及大于 m。这样做即实现了将与分界元素相等的元素聚集在分界元素周围这一效果。三路快速排序在处理含有多个重复值的数组时，效率远高于原始快速排序。其最佳时间复杂度为 O(n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// 模板的 T 参数表示元素的类型，此类型需要定义小于（<）运算
template <typename T>
// arr 为需要被排序的数组，len 为数组长度
void quick_sort(T arr[], const int len) {
  if (len <= 1) return;
  // 随机选择基准（pivot）
  const T pivot = arr[rand() % len];
  // i：当前操作的元素
  // j：第一个等于 pivot 的元素
  // k：第一个大于 pivot 的元素
  int i = 0, j = 0, k = len;
  // 完成一趟三路快排，将序列分为：
  // 小于 pivot 的元素｜ 等于 pivot 的元素 ｜ 大于 pivot 的元素
  while (i < k) {
    if (arr[i] < pivot)
      swap(arr[i++], arr[j++]);
    else if (pivot < arr[i])
      swap(arr[i], arr[--k]);
    else
      i++;
  }
  // 递归完成对于两个子序列的快速排序
  quick_sort(arr, j);
  quick_sort(arr + k, len - k);
}

内省排序

内省排序 是快速排序和 堆排序 的结合。内省排序其实是对快速排序的一种优化，保证了最差时间复杂度为 O(nlog n)。sort() 函数的实现采用了内省排序算法。

1.4 归并排序

归并排序 是高效的基于比较的稳定排序算法。

归并排序最核心的部分是合并（merge）过程：将两个有序的数组 a[i] 和 b[j] 合并为一个有序数组 c[k]。

从左往右枚举 a[i] 和 b[j]，找出最小的值并放入数组 c[k]；重复上述过程直到 a[i] 和 b[j] 有一个为空时，将另一个数组剩下的元素放入 c[k]。

为保证排序的稳定性，前段首元素小于或等于后段首元素时（a[i] <= b[j]）而非小于时（a[i] < b[j]）就要作为最小值放入 c[k]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void merge(const int *a, size_t aLen, const int *b, size_t bLen, int *c) {
  size_t i = 0, j = 0, k = 0;
  while (i < aLen && j < bLen) {
    if (b[j] < a[i]) {  // <!> 先判断 b[j] < a[i]，保证稳定性
      c[k] = b[j];
      ++j;
    } else {
      c[k] = a[i];
      ++i;
    }
    ++k;
  }
  // 此时一个数组已空，另一个数组非空，将非空的数组并入 c 中
  for (; i < aLen; ++i, ++k) c[k] = a[i];
  for (; j < bLen; ++j, ++k) c[k] = b[j];
}

可用 <algorithm> 头文件中的 merge函数：

1
2
3
4
5
6
7
8
merge(iterator beg1, iterator end1, iterator beg2, iterator end2, iterator dest);
//容器元素合并，并存储到另一个容器中
//注意：两个容器必须是有序的
//beg1 容器1开始迭代器
//end1 容器1结束迭代器
//beg2 容器2开始迭代器
//end2 容器2结束迭代器
//dest 目标容器开始迭代器

分治法实现归并排序

  1. 当数组长度为 1 时，该数组就已经是有序的，不用再分解。
  2. 当数组长度大于 1 时，该数组很可能不是有序的。此时将该数组分为两段，再分别检查两个数组是否有序（用第 1 条）。如果有序，则将它们合并为一个有序数组；否则对不有序的数组重复第 2 条，再合并。
1
2
3
4
5
6
7
8
9
10
11
12
void merge_sort(int *a, int l, int r) {
  if (r - l <= 1) return;
  // 分解
  int mid = l + ((r - l) >> 1);
  merge_sort(a, l, mid), merge_sort(a, mid, r);
  // 合并
  int tmp[1024] = {};  // 请结合实际情况设置 tmp 数组的长度（与 a 相同），或使用
                       // vector；先将合并的结果放在 tmp 里，再返回到数组 a
  merge(a + l, a + mid, a + mid, a + r, tmp + l);  // pointer-style merge
  for (int i = l; i < r; ++i) a[i] = tmp[i];
}

1.5 堆排序

堆排序（英语：Heapsort）是指利用 二叉堆 这种数据结构所设计的一种排序算法。堆排序的适用数据结构为数组。堆排序的本质是建立在堆上的选择排序。

首先建立大顶堆，然后将堆顶的元素取出，作为最大值，与数组尾部的元素交换，并维持残余堆的性质；

之后将堆顶的元素取出，作为次大值，与数组倒数第二位元素交换，并维持残余堆的性质；

以此类推，在第 n-1 次操作后，整个数组就完成了排序。

在数组上建立二叉堆

从根节点开始，依次将每一层的节点排列在数组里。

于是有数组中下标为 i 的节点，对应的父结点、左子结点和右子结点如下：

1.6 桶排序

1.7 排序的相关STL

qsort 函数

头文件：<cstdlib>

函数原型：void qsort( void *ptr, size_t count, size_t size,int (*comp)(const void *, const void *) );

qsort 函数有四个参数：数组名、元素个数、元素大小、比较规则。其中，比较规则通过指定比较函数来实现，指定不同的比较函数可以实现不同的排序规则。

比较函数的参数限定为两个 const void 类型的指针。返回值规定为正数、负数和 0。

1
2
3
4
5
6
7
8
9
10
11
12
//比较函数的一种写法
int compare(const void *p1, const void *p2)  // int 类型数组的比较函数
{
  int *a = (int *)p1;
  int *b = (int *)p2;
  if (*a > *b)
    return 1;  // 返回正数表示 a 大于 b
  else if (*a < *b)
    return -1;  // 返回负数表示 a 小于 b
  else
    return 0;  // 返回 0 表示 a 与 b 等价
}

sort 函数

头文件：<algorithm>

1
2
3
4
5
6
// a[0] .. a[n - 1] 为需要排序的数列
// 对 a 原地排序，将其按从小到大的顺序排列
std::sort(a, a + n);

// cmp 为自定义的比较函数
std::sort(a, a + n, cmp);

comp 比较函数对象，在第一参数小于（即先序于）第二参数时返回 true。 bool cmp(const Type1 &a, const Type2 &b);

nth_element 函数

头文件：<algorithm>

用法：

1
2
nth_element(first, nth, last);
nth_element(first, nth, last, cmp);

它重排 [first, last) 中的元素，使得 nth 所指向的元素被更改为 [first, last) 排好序后该位置会出现的元素。这个新的 nth 元素前的所有元素小于或等于新的 nth 元素后的所有元素。此算法是未完成的内省排序。时间复杂度O(n)。

它常用于构建 K-D Tree

partial_sort 函数

头文件：<algorithm>

用法：

1
2
3
// mid = first + k
std::partial_sort(first, mid, last);
std::partial_sort(first, mid, last, cmp);

将序列中前 k 元素按 cmp 给定的顺序进行原地排序，后面的元素不保证顺序。未指定 cmp 函数时，默认按从小到大的顺序排序。

自定义比较

内置类型（如 int）和用户定义的结构体允许定制调用 STL 排序函数时使用的比较函数。可以在调用该函数时，在最后一个参数中传入一个实现二元比较的函数。

对于用户定义的结构体，对其使用 STL 排序函数前必须定义至少一种关系运算符，或是在使用函数时提供二元比较函数。通常推荐定义 operator<。

实例：

1
2
3
4
int a[1009], n = 10;
// ...
std::sort(a + 1, a + 1 + n);                  // 从小到大排序
std::sort(a + 1, a + 1 + n, greater<int>());  // 从大到小排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
struct data {
  int a, b;

  bool operator<(const data rhs) const {
    return (a == rhs.a) ? (b < rhs.b) : (a < rhs.a);
  }
} da[1009];

bool cmp(const data u1, const data u2) {
  return (u1.a == u2.a) ? (u1.b > u2.b) : (u1.a > u2.a);
}

// ...
std::sort(da + 1, da + 1 + 10);  // 使用结构体中定义的 < 运算符，从小到大排序
std::sort(da + 1, da + 1 + 10, cmp);  // 使用 cmp 函数进行比较，从大到小排序

前缀和

定义：数列的前n项和，是一种重要的预处理方式，能大大降低查询时间的复杂度。

C++ 标准库中实现了前缀和函数 partial_sum，定义于头文件 <numeric>。

一维前缀和

原数组：A[N]，前缀和数组：B[N]

递推公式：B[0] = A[0]，对于 i>0，则B[i] = B[i-1] + A[i]。

二维/多维前缀和

普遍求解方法几乎店铺是容斥原理。

一维前缀和拓展到二维前缀和

示例：比如我们有这样一个矩阵 a，可以视为二维数组：

1
2
3
1 2 4 3
5 1 2 4
6 3 5 9

我们定义一个矩阵 使得 ， 那么这个矩阵长这样：

1
2
3
1  3  7  10
6  9  15 22
12 18 29 45

第一个问题就是递推求 的过程，。

因为同时加了 和 ，故重复了 ，减去。

第二个问题就是如何应用，譬如求 子矩阵的和。

类似的，易得答案为 。

例题：

洛谷 P1387 最大正方形

在一个 n*m 的只包含 0 和 1 的矩阵里找出一个不包含 0 的最大正方形，输出边长。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <algorithm>
#include <iostream>
using namespace std;
int a[103][103];
int b[103][103];  // 前缀和数组，相当于上文的 sum[]

int main() {
  int n, m;
  cin >> n >> m;

  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
      cin >> a[i][j];
      b[i][j] =
          b[i][j - 1] + b[i - 1][j] - b[i - 1][j - 1] + a[i][j];  // 求前缀和
    }
  }

  int ans = 1;

  int l = 2;
  while (l <= min(n, m)) {  // 判断条件
    for (int i = l; i <= n; i++) {
      for (int j = l; j <= m; j++) {
        if (b[i][j] - b[i - l][j] - b[i][j - l] + b[i - l][j - l] == l * l) {
          ans = max(ans, l);  // 在这里统计答案
        }
      }
    }
    l++;
  }

  cout << ans << endl;
  return 0;
}

另一种基于容斥原理的做法，可以降低时间复杂度。

1
2
3
4
5
6
7
8
9
for(int i=1;i<=n;++i)
	S[i]=S[i-1]+A[i];
	
for(int i=1;i<=n;++i)
	for(int j=1;j<=n;++j)
		S[i][j]=S[i][j-1]+A[i][j];
for(int i=1;i<=n;++i)
	for(int j=1;j<=n;++j)
		S[i][j]=S[i-1][j]+S[i][j];

这种写法的思想其实就是一维一维的统计，这样的统计方法，复杂度就降到

基于 DP 计算高维前缀和

基于 容斥原理 来计算 高维前缀和的方法，形式简单，但当维数升高时，起复杂度较高。所以有另一种写法，结合位运算能在高维前缀和统计时降低复杂度。SOS DP

设高维空间 U 共有 D 维，需要对 求高维前缀和 。令 表示同 后 D - i 维相同的所有点对于 点高维前缀和的贡献。由定义可知 ，以及 。

其递推关系为 = ，其中 为第 i 维恰好比 少 1 的点。该方法的复杂度为 ，其中 |U| 为高维空间 U 的大小。

伪代码：

1
2
3
4
5
for state
  sum[state] = f[state];
for(i = 0;i <= D;i += 1)
  for 以字典序从小到大枚举 state
    sum[state] += sum[state'];

计算一维前缀和

1
2
3
4
5
6
7
//内存优化，超级容易编码
for(int i = 0; i<(1<<N); ++i)
    F[i] = A[i];
for(int i = 0;i < N; ++i) for(int mask = 0; mask < (1<<N); ++mask){
    if(mask & (1<<i))
        F[mask] += F[mask^(1<<i)];
}

举例子：对于 ∀i,i∈[1,n] 都有一个权值 ，对于每一个 i ，请你输出 。。换句话说，对于每一个 i，找出所有二进制下与 i 相同或者是 i 的子集的数 j，将这些数的权值 加起来，就是 的值。

将数 i 转化为 二进制形式，以 0110101 为例，可以将其看成 7 维的坐标，然后 该数的权值就是这个坐标的权值，对于 0110101 来说，我们要统计所有坐标中 满足每一维度的坐标小于等于 0110101 每一维度的坐标的 权值和。

差分

差分 是一种和前缀和相对的策略，可以当作是求和的逆运算。

这种策略的定义是令

性质

  • 的值是 的前缀和，即
  • 计算 的前缀和

它可以维护多次对序列的一个区间加上一个数，并在最后询问某一位的数或是多次询问某一位的数。注意修改操作一定要在查询操作之前。

譬如使 [l,r] 中的每个数加上一个 k，即 其中 ，

最后做一遍前缀和就好了。

C++ 标准库中的 差分函数：adjacent_difference，定义于头文件<numeric>中。

树上差分

树上差分可以理解为对树上的某一段路径进行差分操作，这里的路径可以类比一维数组的区间进行理解。例如在对树上的一些路径进行频繁操作，并且询问某条边或者某个点在经过操作后的值的时候，就可以运用树上差分思想了。

树上差分通常会结合 树基础 和 最近公共祖先 来进行考察。树上差分又分为 点差分 与 边差分，在实现上会稍有不同。

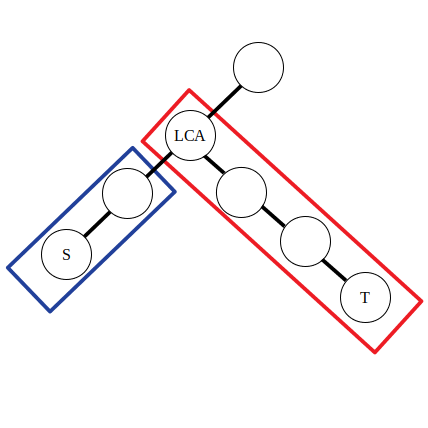
点差分

举例：对树上的一些路径 进行访问，问一条路径 上的点被访问的次数。

对于一次 的访问，需要 找到 s 与 t 的公共祖先，然后对这条路径上的点进行访问（点的权值加一），若采用 DFS 算法对每个点进行访问，由于有太多的路径需要访问，时间上承受不了。这里进行 差分操作：

其中 f(x) 表示 x 的父亲节点， 为点权 的差分数组。

img

可以认为公式中的前两条是对蓝色方框内的路径进行操作，后两条是对红色方框内的路径进行操作。不妨令 左侧的直系子节点为 。那么有 ，。可以发现实际上点差分的操作和上文一维数组的差分操作是类似的。

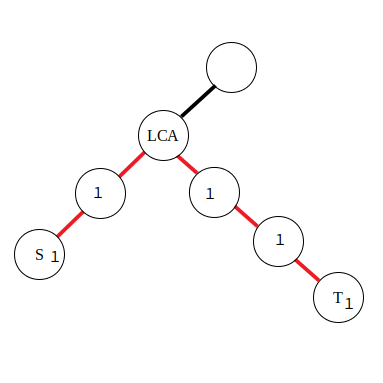
边差分

若是对路径中的边进行访问，就需要采用 边差分 策略了，使用以下公式： img

由于在边上直接进行差分比较困难，所以将本来应当累加到红色边上的值向下移动到附近的点里，那么操作起来也就方便了。对于公式，有了点差分的理解基础后也不难推导，同样是对两段区间进行差分。

例题

Monitor HDU - 6514

题意：小腾有n∗m的田地，但是有小偷来偷东西，在一片矩形区域上，有一部分区域是监控可以覆盖到的，这部分区域由一个或多个包含于该矩形区域的小矩形构成；现在给你另一个包含在该矩形区域的小矩形A，问你这个小矩形能否被监控完全覆盖。

普通暴力解法，三层循环必然导致 超时。

应采用 前缀和+差分的知识 去解题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>

using namespace std;
typedef long long ll;

int main()
{
    int n, m;
    while(~scanf("%d%d", &n, &m))
    {
        vector<vector<int>> f(n + 10, vector<int>(m + 10, 0));
        
        int p;
        scanf("%d", &p);
        while(p--)
        {
            // 给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上1
            int x1, y1, x2, y2;
            scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
            f[x1][y1]++;
            f[x2 + 1][y1]--;
            f[x1][y2 + 1]--;
            f[x2 + 1][y2 + 1]++;
        }
        
        // 求差分数组的前缀和，得到原数组的值
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= m; j++)
                f[i][j] += f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1];
        
        // 如果被监控覆盖了多次，则只记一次
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= m; j++)
                if(f[i][j] > 1) f[i][j] = 1;
        //再处理前缀和
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= m; j++)
                f[i][j] += f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1];
        
        int q;
        scanf("%d", &q);
        while(q--)
        {
            int x1, y1, x2, y2;
            scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
            
            int t1 = (x2 - x1 + 1) * (y2 - y1 + 1);
            int t2 = f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1];
            
            if(t1 == t2)    puts("YES");
            else    puts("NO");
        }
    }
    
    return 0;
}

SOS DP 基于 DP 计算高维前缀和

Compatible Numbers

题目大意：对于一个数 x 找和它相与值为0的数，可以先将 x 按位取反，将取反得到的数记为y，将要找的与x值为0的数记为z，那么y的二进制中，若某一位为0，z的这一位也要是0，若y的某一位为1，那么z的这一位可以是0也可以是1，这类似于一个 高维的前缀和。查找z的过程就是看 前缀和y是否为0。

设 f[state] 表示 state 这个状态能否由 中某一个的二进制的某些位 从0变成1 得来，g[state] 则用来记录这个 state 是由哪个初始的 变化而来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<iostream>
using namespace std;
const int N = 1e6+10;
int n;
int A[N] , f[1 << 22] , g[1 << 22];
int main()
{
	cin >> n;
	for(int i = 1 ; i <= n ; ++i)
		cin >> A[i]; //获取数组
	for(int i = 1 ; i <= n ; ++i)
		f[A[i]] = 1 , g[A[i]] = A[i];
	for(int i = 0 ; i < (1 << 22) ; ++i) if(f[i])
	{
		for(int j = 0 ; j < 22 ; ++j)
			if(!(i & (1 << j)))
				f[i | (1 << j)] = 1 , g[i | (1 << j)] = g[i];
	}
	for(int i = 1 ; i <= n ; ++i)
	{
		int y = (~A[i]) & ((1 << 22) - 1);
		if(f[y])
			cout << g[y] << ' ';
		else
			cout << -1 << ' ';
	}
	return 0;
}
  • 标题: 算法基础
  • 作者: 卡布叻_米菲
  • 创建于 : 2023-04-11 22:50:00
  • 更新于 : 2024-02-08 11:44:32
  • 链接: https://carolinebaby.github.io/2023/04/11/算法基础/
  • 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
评论
此页目录
算法基础
  1. 1 排序
    1. 1.1 计数排序
    2. 1.2 基数排序
    3. 1.3 快速排序
    4. 1.4 归并排序
    5. 1.5 堆排序
    6. 1.6 桶排序
    7. 1.7 排序的相关STL
  2. 前缀和
    1. 一维前缀和
    2. 二维/多维前缀和
  3. 差分
    1. 树上差分
    2. 例题